Réseau de Petri - Définition

Introduction

Exemple d'un réseau de Petri Place-Transition, composé de :

• deux places, les cercles
• trois transitions, les traits noirs
• quatre arcs, les flèches
• deux jetons, les points noirs qui circulent de gauche à droite

Un réseau de Petri (en français on prononce [petʁi̩] ) est un modèle mathématique servant à représenter divers systèmes (informatiques, industriels,…) travaillant sur des variables discrètes.

Histoire

Le problème du diner des philosophe modélisé en Réseau de Petri

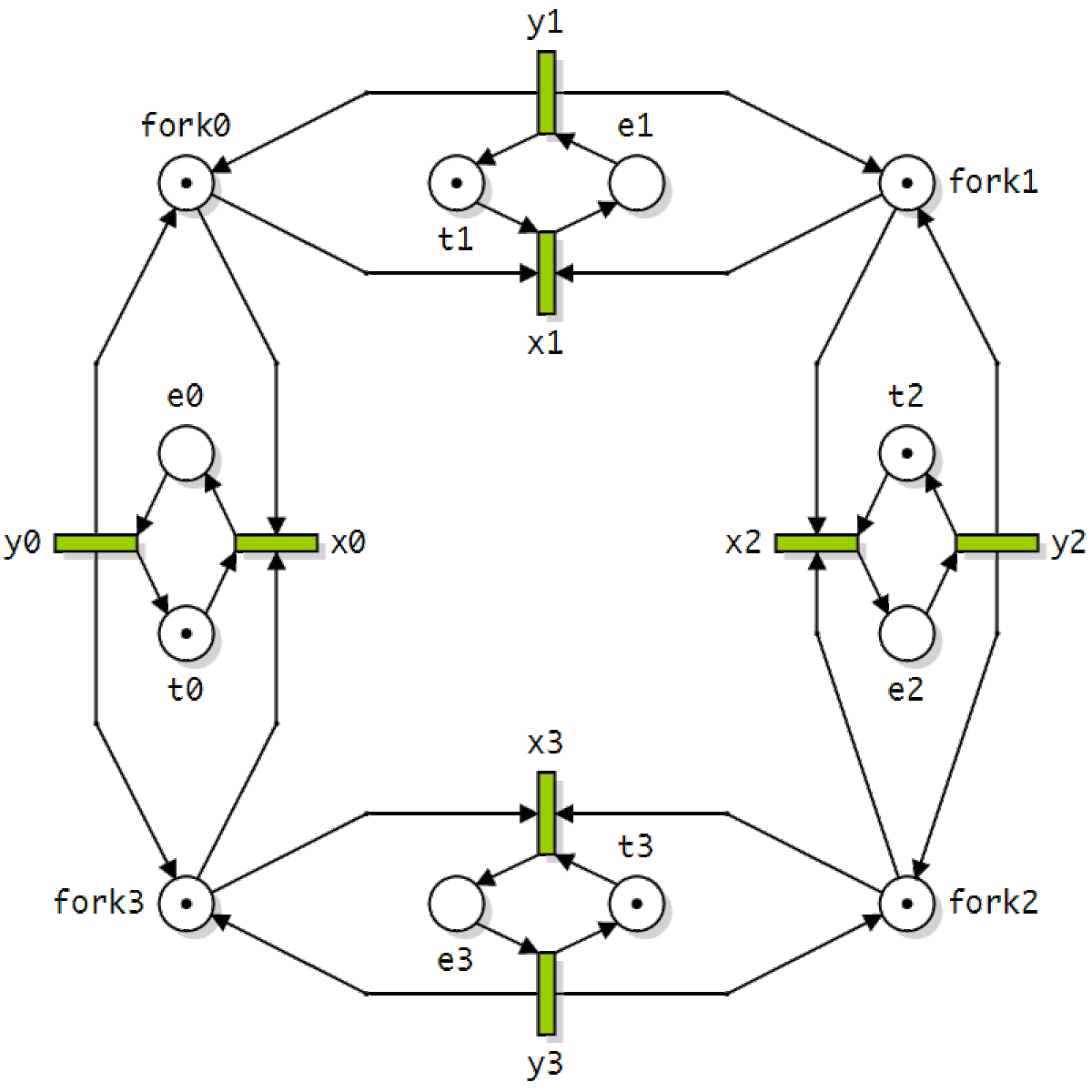
Les réseaux de Petri sont apparus en 1962, dans la thèse de doctorat de Carl Adam Petri.

Représentation

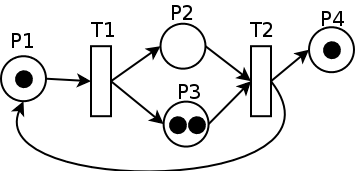
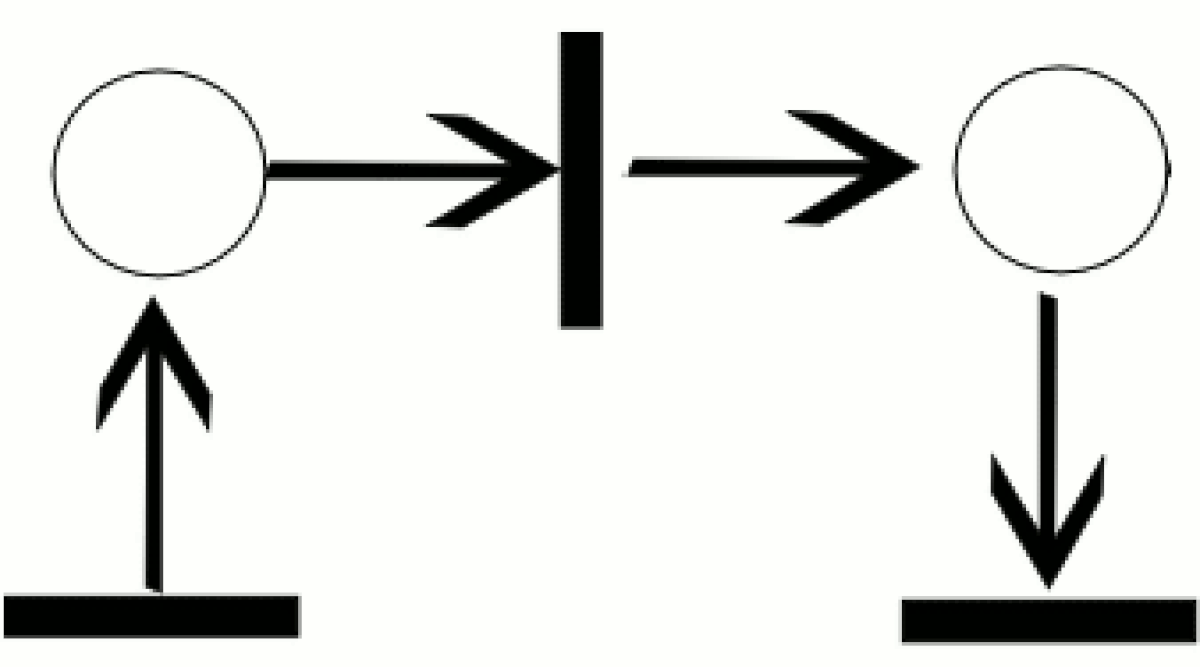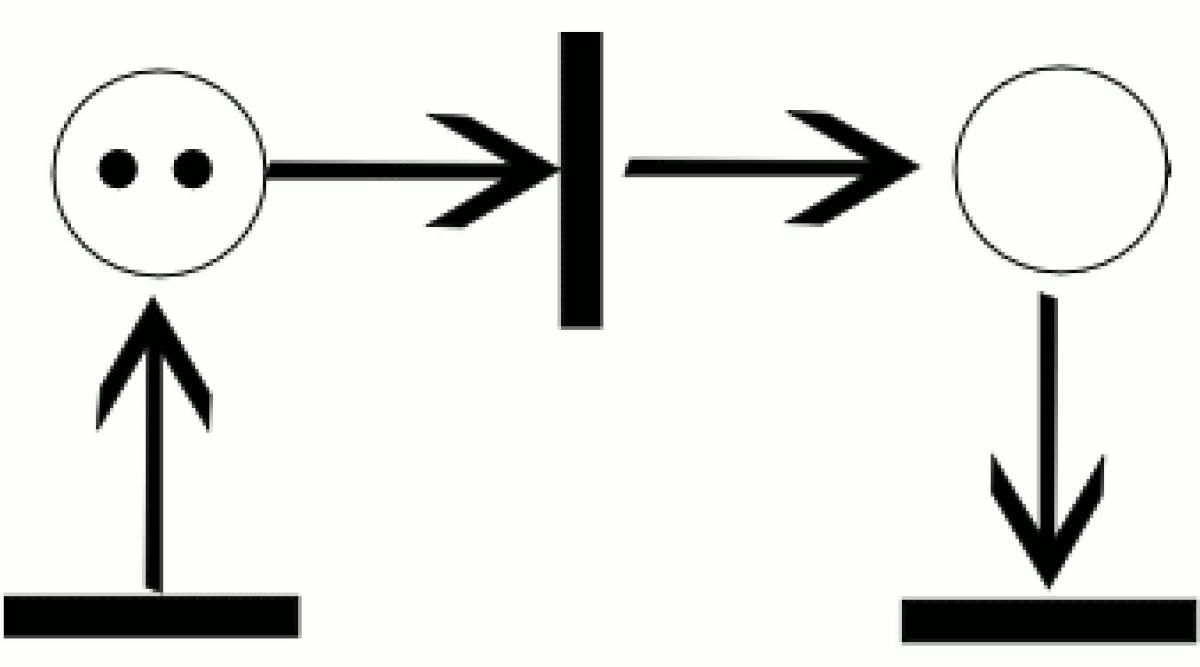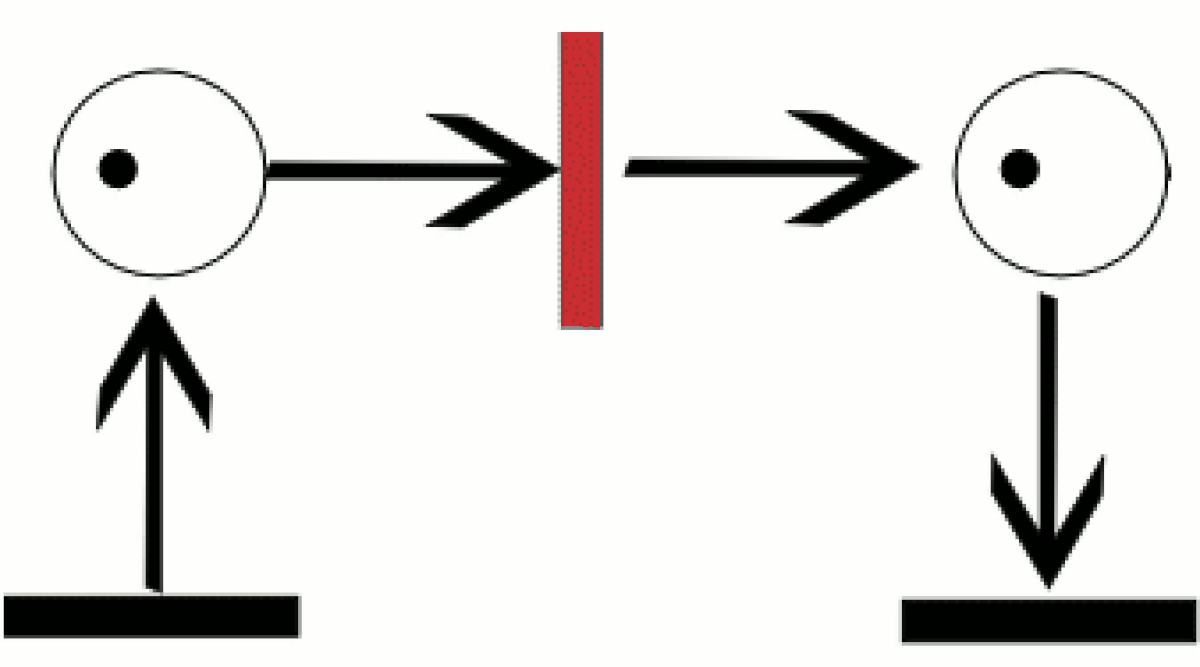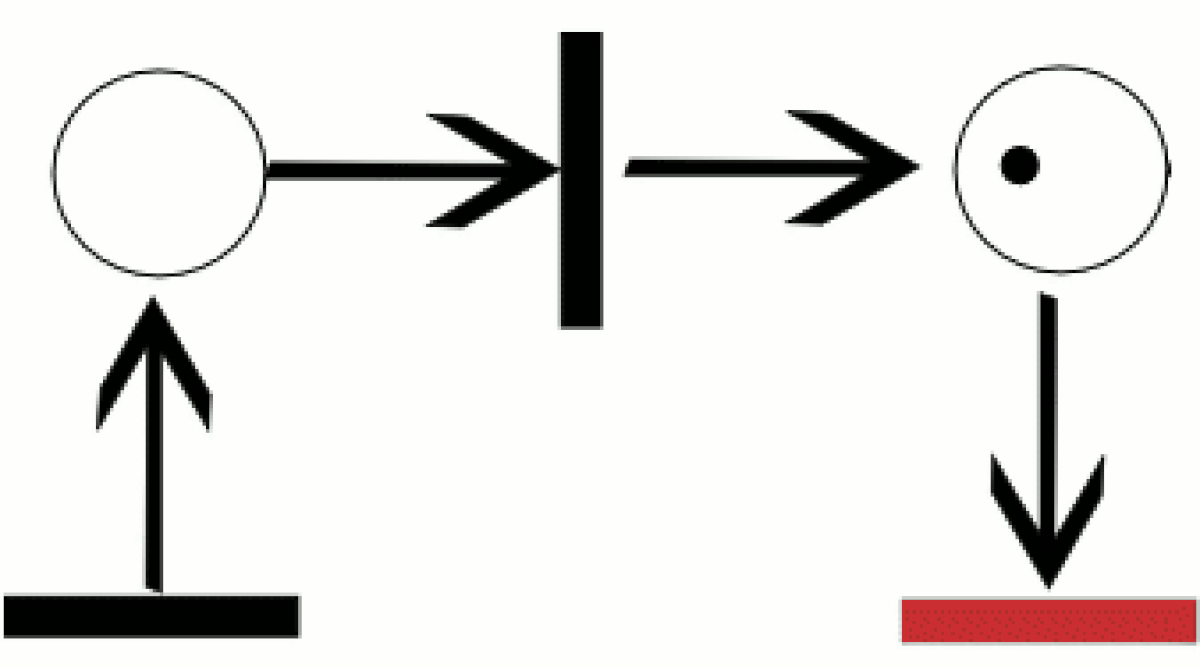
Un réseau de Petri se représente par un graphe biparti (composé de deux types de nœuds et dont aucun arc ne relie deux nœuds de même type) orienté (composé d'arc(s) ayant un sens) reliant des places et des transitions (les nœuds). Deux places ne peuvent pas être reliées entre elles, ni deux transitions. Les places peuvent contenir des jetons, représentant généralement des ressources disponibles.

La distribution des jetons dans les places est appelée le marquage du réseau de Petri.

Les entrées d'une transition sont les places desquelles part une flèche pointant vers cette transition, et les sorties d'une transition sont les places pointées par une flèche ayant pour origine cette transition.

Représentation matricielle

La définition matricielle introduit les matrices et .

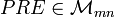
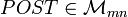
• PRE_pt = W(p,t)
• POST_pt = W(t,p)

Ces matrices de même dimension représentent en ligne les places, et en colonne les transitions. PRE contient les valuations des arcs qui vont des places vers les transitions, POST concerne les arcs des transitions vers les places. Une valeur nulle dans une des matrices indique l'inexistence d'un arc dans un sens ou dans l'autre.

La matrice d'incidence C est définie par C = POST − PRE. Étant donnée une transition t, C_pt est le nombre de jetons qui seront ajoutés (ou retirés si le nombre est négatif) à la place p si la transition t est franchie.

Définition

Un réseau de Petri est un 6-uplet , où (cf. Desel et Juhás)

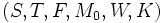
• S définit une ou plusieurs places.
• T définit une ou plusieurs transitions.
• F définit un ou plusieurs arcs (flèches).

Un arc ne peut pas être connecté entre 2 places ou 2 transitions ; plus formellement : .

• appelé marquage initial, où, pour chaque place , il y a jetons.
• appelé ensemble d'arcs primaires , assignant à chaque arc un entier positif qui indique combien de jetons sont consommés depuis une place vers une transition, ou sinon, combien de jetons sont produis par une transition et arrivent pour chaque place.
• appelé limite de capacité, faisant correspondre à chaque place un nombre positif représentant le nombre maximum de jetons qui peuvent occuper une place.

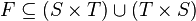
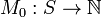
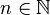
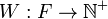
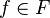
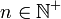
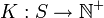
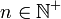
De nombreuses définitions formelles existent. Cette définition concerne un réseau place-transition (ou P-T). D'autres définitions n'incluent pas la notion d'arc primaire ou la limite de capacité.

Extensions

Un réseau de Petri de haut niveau est un réseau coloré et hiérarchique.

Couleur

Pour un réseau de Petri de base, on ne distingue pas les différents jetons. Dans un réseau de Petri coloré, on associe une valeur à chaque jeton.

Pour plusieurs outils associés aux réseaux de Petri colorés, les valeurs des jetons sont typées, et peuvent être testées et/ou manipulées avec un langage fonctionnel.

Hiérarchie

Une autre extension du réseau de Petri est la hiérarchie (ou récursivité) : des éléments du réseau de Petri sont eux-mêmes composés d'un réseau de Petri.

Stochastique

Les réseaux de Petri Stochastiques ajoutent de l'indéterminisme et des probabilités de tir.