Samedi 14 Juin 2025
Rechercher 🔍

Semi-norme - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Définition et exemples - Norme et espace quotient - Propriétés - Topologie définie par une famille de semi-normes - Espace localement convexe - Famille filtrante de semi-normes

Famille filtrante de semi-normes

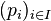
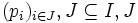
Une famille (p_i)_{i \in I} de semi-normes sur l'espace vectoriel E est dite filtrante si pour toute sous-famille finie (p_i)_{i \in J}, J \subseteq I, J finie, il existe une semi-norme p de la famille majorant toutes les semi-normes de J.

Exemple 1: La famille de semi-normes définie précédemment n'est pas filtrante. Cependant on peut toujours définir une famille filtrante en effectuant une "complétion" comme montré ci-après.

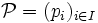
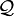
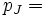
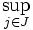
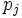
Exemple 2 ("complétion" d'une famille quelconque): Soit une famille quelconque \mathcal P=(p_i)_{i \in I} de semi-normes sur E. On peut alors définir la famille \mathcal Q dont les éléments sont définis par \quad p_J= \sup_{j \in J} \quad p_j , J sous-famille finie de I.

On voit facilement alors que \mathcal Q est une famille filtrante de semi-normes.

Topologie définie par une famille de semi-normes - Espace localement convexe
- Introduction - Définition et exemples - Norme et espace quotient - Propriétés - Topologie définie par une famille de semi-normes - Espace localement convexe - Famille filtrante de semi-normes
miniature
💥 La collision entre notre Voie lactée et la galaxie d'Andromède remise en question
miniature
🎶 Pourquoi les oiseaux chantent-ils autant et si fort au printemps ?
miniature
💡 Générer de la lumière à partir du vide, c'est possible
miniature
Découverte d'un deuxième système d'apprentissage dans le cerveau
miniature
☀️ Comment se produit un coup de chaleur et comment s'en protéger ?
miniature
⚽ Comment fonctionne la physique d'un tir puissant au foot ?
miniature
🧠 Un algorithme révèle comment notre cerveau se motive
miniature
🔭 Une si grande planète orbite une si petite étoile, comment est-ce possible ?
miniature
1
🐋 Les baleines développent de nouvelles méthodes pour communiquer avec nous
miniature
🥚 Le noyau de Mars sent l'œuf pourri
miniature
🧠 On sait enfin pourquoi le sémaglutide fait maigrir
miniature
🌱 La vie pourrait renaître sur Europe après la mort de la Terre
miniature
🌿 Confirmation scientifique: ce remède ancestral fait naturellement maigrir, et pas qu'un peu !
miniature
💥 Des astronomes identifient les plus puissantes explosions depuis le Big Bang
miniature
🦕 Ce crâne de stégosaure, le plus complet jamais découvert, réécrit l'histoire
miniature
🛏️ Les punaises de lit, ces compagnons indésirables depuis la préhistoire
miniature
🕸️ Connaissez-vous la toile cosmique, l'architecte de l'Univers ?
miniature
🌋 L'éruption de l'Etna vue depuis l'espace
miniature
🐋 Il y a 20 000 ans, l'Homme fabriquait des outils avec des os de baleines
miniature
🟠 Quel est le rôle de ce labyrinthe sur Mars ?
miniature
🎯 Cette stratégie innovante contre le cancer du sein offre une survie de 100%
miniature
1
💥 Le pulsar à trou noir: un objet qui intrigue les astrophysiciens
miniature
🐒 Première: ces singes kidnappent les bébés d'une autre espèce
miniature
🌍 Découverte d'une super-Terre à l'habitabilité intermittente
miniature
🧠 Ces cellules pourraient jouer un rôle bien plus important que les neurones dans la mémoire
miniature
🛰️ Une carte photographique de la Terre toutes les 35 minutes
miniature
Pourquoi l'oxygène est-il si indispensable à autant d'êtres vivants ?
miniature
🐱 Pourquoi certains chats miaulent et ronronnent plus que d'autres ?
miniature
Découverte: un antidouleur sans effets secondaires
miniature
1
🤔 Ces expériences remettent en question un concept fondamental de la thermodynamique
miniature
Le cannabis réduit de moitié la fonction des vaisseaux sanguins
miniature
Les différences hommes-femmes ne sont pas que génétiques
miniature
🦴 Des paresseux géants de plusieurs tonnes parcouraient autrefois l'Amérique
miniature
James Webb découvre une nouvelle population de trous noirs supermassifs
miniature
Le sol de l'Afrique du Sud s'est soulevé ces dernières années, pourquoi ?
miniature
👀 Ces lentilles de contact permettent de voir l'invisible
miniature
Révélations sur l'histoire de la lèpre en Amérique
miniature
Ce nouveau matériau possède des propriétés jamais vues !
miniature
😂 Que savons-nous réellement sur les chatouilles ?
miniature
1
Pour la lumière, le temps n'existe pas 🌟
miniature
Des scientifiques mesurent un ralentissement du vieillissement lié à ce cocktail
miniature
La tension de Hubble, mystère de l'expansion de l'Univers, enfin résolue ?
miniature
Voici comment les graisses saturées endommagent votre intestin en seulement deux jours
miniature
1
Les scientifiques réfléchissent à rendre Mars habitable
miniature
Cette empreinte digitale a 43 000 ans 🖐️
miniature
Un objet inconnu émet dans l'espace des signaux avec une régularité jamais vue 🛰
miniature
Comment la peste a évolué pour durer
miniature
Un indice de plus qu'Europe, lune de Jupiter, cacherait un océan salé sous sa glace
miniature
Le changement climatique menace l'accès à l'eau de 2 milliards de personnes
miniature
Le noyau de la Terre perd son or... qui remonte jusqu'en surface 🌍
Page générée en 0.074 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise