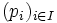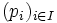Semi-norme - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Topologie
A l'instar de la norme, une semi-norme définit une topologie pour laquelle les boules ouvertes de centre un point x forment une base de voisinages de x : un ensemble O est ouvert si, pour chaque point x de O, il existe une boule ouverte non vide de centre x incluse dans O. Cette topologie est séparée si et seulement si la semi-norme vérifie la propriété de séparation, c'est-à-dire si la semi-norme est une norme.
Pour cette topologie, l'addition et la multiplication par un scalaire sont continues : on dit que l'espace vectoriel E, muni de cette topologie, est un espace vectoriel topologique. La semi-norme, elle aussi, est continue. Par ailleurs, les boules sont convexes.
Les démonstrations sont analogues à celles proposées dans l'article Norme (mathématiques).
Noyau
Les vecteurs de semi-norme nulle jouent un rôle particulier, ce rôle justifie la définition suivante :
Définition — L'ensemble des vecteurs de semi-norme nulle s'appelle le noyau de la semi-norme.
Le noyau possède des propriétés à la fois algébriques et topologiques :
Proposition — Le noyau d'une semi-norme est un sous-espace vectoriel fermé. Il est égal à l'adhérence du vecteur nul.
En effet, un vecteur x est adhérent au vecteur nul si et seulement si toute boule ouverte de centre x et de rayon r>0 contient ce vecteur nul, ce qui se traduit par : la semi-norme de x est inférieure à tout r>0, ou encore : x appartient au noyau. Ceci prouve que le noyau est bien l'adhérence du vecteur nul. C'est donc un sous-espace vectoriel fermé (comme l'est toute adhérence d'un sous-espace vectoriel dans un espace vectoriel topologique).
Cône des semi-normes
La somme de deux semi-normes est une semi-norme. Il en est de même pour la multiplication externe par un scalaire positif. On en déduit que les semi-normes forment un convexe.
Proposition — L'ensemble des semi-normes sur un espace E est un cône convexe d'extrémité la fonction nulle, de l'ensemble des applications de E dans R. Ce cône est stable pour l'addition.
Topologie définie par une famille de semi-normes - Espace localement convexe
- Soit E un espace vectoriel réel ou complexe muni d'une famille filtrante
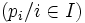
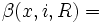
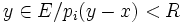
Autrement dit les voisinages de x sont les ensembles contenant au moins une "p-boule".
Vérifions que les 4 axiomes des voisinages sont bien vérifiés:
- Tout voisinage de x contient x (évident ici).
- Si
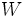
- L'intersection de 2 voisinages de x est un voisinage de x (en effet si
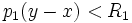
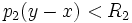
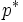
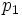
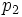
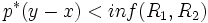
- Il existe un voisinage de x qui soit voisinage de chacun de ses points. En fait toute "p-boule" est voisinage de chacun de ses points puisque si y est un point de la "p-boule"
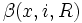
 tel que
tel que
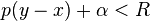
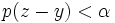
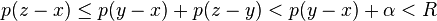
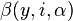
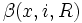
- Démontrons maintenant que la topologie que nous venons de définir est compatible avec la structure d'espace vectoriel, ce qui fait de E un espace vectoriel topologique . Un tel espace est dit espace localement convexe.
- L'application
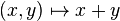
En effet un voisinage de x+y contient la "p-boule"
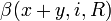
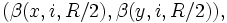
- L'application
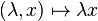
En effet un voisinage de λx contient la "p-boule"
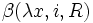
![(]-\sqrt R,\sqrt R[,\beta (x,i,\sqrt R))](https://static.techno-science.net/illustration/Definitions/autres/9/9940b19cb6f80c9219503bb937f53159_d8e0b42fe0ebe1e182f59e71218775ac.png)
- Plus généralement, si