Semi-norme - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une semi-norme est une application d'un espace vectoriel dans l'ensemble des réels positifs. Elle dispose presque des propriétés lui conférant le statut de norme. Une propriété est manquante, la semi-norme d'un vecteur non nul n'est pas nécessairement non nulle.
En analyse fonctionnelle, cette situation est relativement courante. L'espace vectoriel est un espace de fonctions d'un ouvert d'un espace vectoriel topologique de dimension finie à valeur dans les réels ou complexes. La semi-norme correspond par exemple à l'intégrale de la valeur absolue ou du module de la fonction. Une fonction nulle sur l'ouvert sauf sur un ensemble négligeable est non nulle mais de semi-norme nulle.
La topologie induite par la semi-norme confère à l'espace le statut d'espace vectoriel topologique. Il possède néanmoins une faiblesse rendant malcommode son usage. l'espace n'est pas séparé. En vue de pallier cette difficulté, il est toujours possible de quotienter l'espace pour obtenir un nouvel ensemble équipé d'une structure d'espace vectoriel normé. En termes d'analyse fonctionnelle, ce quotient revient à travailler non plus sur des fonctions, mais sur des classes de fonctions, équivalentes donc identifiées si elles ne diffèrent que sur un ensemble négligeable.
Définition et exemples
Définition
Dans cet article, E désigne un espace vectoriel sur un corps K. En général K désigne le corps des réels ou des complexes, même si la théorie s'applique dans un contexte plus général. L'espace E est muni d'une semi-norme N. La lettre Ω désigne un ouvert de Kn où n est un entier strictement positif, Kn est muni de sa topologie naturelle et μ une mesure sur Ω. E' désigne le dual topologique de E et σ (E, E' ) la topologie faible de E.
Définition — Une semi-norme sur E est une application N de E dans l'ensemble des nombres réels positifs vérifiant les axiomes dit d'homogénéité et de sous-additivité. Ils s'expriment de la manière suivante:
- homogénéité :
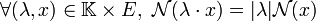
- sous-additivité :
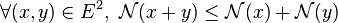
La propriété manquante est celle de la séparation, qui assure que la norme d'un vecteur est nulle seulement si le vecteur est nul. Cette propriété confère à la semi-norme le statut de norme.
- séparation :
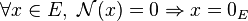
Exemples
Deux configurations introduisent naturellement une semi-norme en analyse fonctionnelle :
L'ensemble des fonctions intégrables en valeur absolue ou en module de Ω dans K pour la mesure μ est un espace vectoriel noté L1(Ω) et possédant la semi-norme N1 définie de la manière suivante :
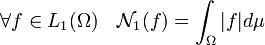
La propriété de séparation est absente, toute fonction nulle sauf sur un ensemble négligeable possède une norme nulle.
Un deuxième exemple provient de la topologie faible. Soit e' un élément de E' c'est-à-dire une forme linéaire continue de E. L'application pe', définie de la manière suivante est une semi-norme :
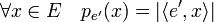
Cette semi-norme est nulle sur un hyperplan fermé, le noyau de e' .
Norme et espace quotient
Soit H le sous-espace des vecteurs de semi-norme nulle de E. D'après l'inégalité triangulaire, la semi-norme est constante sur chaque classe du quotient E/H. On peut donc équiper ce quotient d'une norme induite en posant :
Définition — Si H est le noyau d'une semi-norme
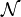
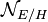
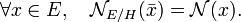
Comme il est infiniment plus pratique de travailler sur un espace séparé, cette technique de quotient est largement utilisée, par exemple en analyse fonctionnelle. Soit Lp(Ω,μ) l'espace des fonctions de Ω dans K dont le module à la puissance p est intégrale sur Ω pour la mesure μ. Ici p désigne un réel compris entre un et l'infini. Cet espace est presque dénommé l'espace Lp de Ω.
La norme est définie par l'égalité suivante :
![\forall f \in L^p(\Omega,\, \mu) \quad \|f\|_p = {\left[\int_{\Omega} |f|^p d\mu\right]}^{1/p}](https://static.techno-science.net/illustration/Definitions/autres/0/048b99e68a4ffd98412055185b5fe806_40221f4851d89036725e0c615b565ec9.png)
Alors le noyau de la semi-norme est l'ensemble des fonctions nulles sur Ω sauf, peut être sur un ensemble négligeable. En pratique Lp(Ω,μ) est déjà quotienté par le noyau de la semi-norme, il est donc équipé d'une norme.

















































