Symétrie (transformation géométrique) - Définition
La liste des auteurs de cet article est disponible ici.
Symétrie dans l’espace
Symétrie centrale
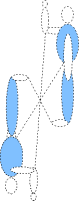
On retrouve la même définition et les mêmes propriétés que pour la symétrie centrale dans le plan, à ceci près qu’une symétrie centrale ne conserve pas l’orientation dans l’espace.
Le bonhomme lève la main droite et son image lève la main gauche.
Symétrie orthogonale par rapport à une droite
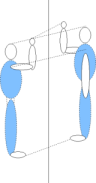
On retrouve la même définition que dans le plan. Une symétrie orthogonale par rapport à une droite est aussi une rotation d’axe (d) et d’angle plat.
Contrairement à ce qui se passe dans le plan, une telle symétrie dans l’espace conserve l’orientation.
Le bonhomme lève la main droite et son image lève la main droite.
Symétrie orthogonale par rapport à un plan
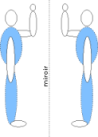
La symétrie orthogonale par rapport au plan (P) est la transformation qui laisse tous les points de (P) invariants et qui, à tout point M non situé sur (P), associe le point M’ tel que (P) soit le plan médiateur de [MM']
Une telle symétrie conserve les distances et les angles mais ne conserve pas l'orientation. C'est la raison pour laquelle, quand vous levez la main droite devant votre miroir, votre image lève sa main gauche.
On démontre que l'ensemble des symétries par rapport à des plans génère par composition tout l'ensemble des isométries de l'espace
Les symétries obliques
On peut tout aussi bien définir des symétries d’axe (d) selon la direction (P) ou des symétries par rapport à (P) suivant la direction (d), à condition que tout sous-espace égal ou parallèle à (P) ne contienne pas entièrement (d) ni ne soit entièrement contenu dans (d) et que leur intersection se réduise à un seul point (sinon ces transformations ne sont pas des symétries mais des projections).
Mais ces transformations ne sont pas des isométries si (d) et (P) ne sont pas orthogonaux. Ces transformations (de même que les projections) conservent cependant les barycentres et sont des cas particuliers de transformations affines de l’espace.

















































