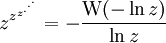Tétration - Définition

Tours de puissance infiniment hautes

converge vers 2, et peut être en réalité définie comme étant égale à 2. La tendance vers 2 peut être perçue en évaluant une petite tour finie : .

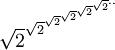
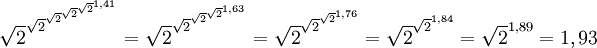
En général, la tour de puissance infinie converge si et seulement si . Pour un réel quelconque r avec , puis x = r^{1 / r}, alors la limite est r (démonstration).

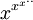
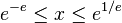
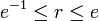
Cela peut être étendu aux nombres complexes z avec la définition :

où W(z) est la fonction W de Lambert.