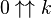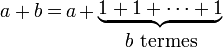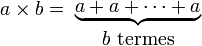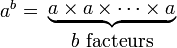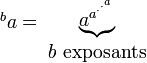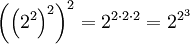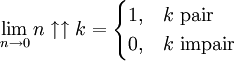Mercredi 23 Avril 2025
Rechercher 🔍

Tétration - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Notation - Extension aux valeurs faibles du second opérand - Exemples - Extension aux nombres réels - Tétration complexe - Tours de puissance infiniment hautes

Introduction

La tétration (ou encore nappe exponentielle, hyperpuissance, tour de puissance, super-exponentiation ou hyper4) est une « exponentiation itérative », le premier hyper opérateur après l'exponentiation.

Le mot-valise tétration a été forgé par Reuben Goodstein sur la base du préfixe tétra- (quatre) et itération. La tétration est utilisée pour l'écriture des grands nombres. Elle suit l'addition, la multiplication et l'exponentiation comme indiqué ci-après :

  1. addition
    {{a + b} \atop \,} {= \atop \,} {a \, + \atop \, } {{\underbrace{1 + 1 + \cdots + 1}} \atop b \text{ termes}}
  2. multiplication
    {{a \times b = \ } \atop {\ }} {{\underbrace{a + a + \cdots + a}} \atop b\text{ termes}}
  3. exponentiation
    {{a^b = \ } \atop {\ }} {{\underbrace{a \times a \times \cdots \times a}} \atop b\text{ facteurs}}
  4. tétration
    {\ ^{b}a = \ \atop {\ }} {{\underbrace{a^{a^{\cdot^{\cdot^{a}}}}}} \atop b\text{ exposants}}

chaque opération étant définie par itération à partir de la précédente.

L'addition (a+b) peut être définie comme b itérations de l'opération ajouter 1 appliquée à a, la multiplication (a.b) comme b itérations de l'opération ajouter a appliquée à a, et l'exponentiation (ab) comme b itérations de l'opération multiplier par a appliquée à a. De manière analogue, la tétration (ba) peut être considérée comme b itérations de l'opération porter à la puissance a appliquée à a.

On remarquera que lorsque l'on évalue une exponentiation à niveaux multiples, l'exponentiation est effectuée à un niveau le plus « profond » en premier lieu (en notation, au niveau le plus élevé). En d'autres termes :

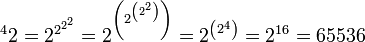
\,\!\ ^{4}2 = 2^{2^{2^2}} = 2^{\left(2^{\left(2^2\right)}\right)} = 2^{\left(2^4\right)} = 2^{16} = 65536
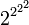
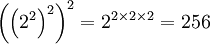
\,\!2^{2^{2^2}} n'est pas égal à \,\! \left({\left(2^2\right)}^2\right)^2 = 2^{2\times2\times2} = 256 .

Ceci est la règle générale pour l'ordre des opérations impliquant une exponentiation répétée.

Notation

Afin de généraliser le premier cas au-dessus (tétration), une nouvelle notation est nécessaire (voir ci-dessous); cependant, le second cas peut-être également écrit :

\,\! \left(\left(2^2\right)^2\right)^2 = 2^{2 \cdot 2 \cdot 2} = 2^{2^3}

Donc, sa forme générale utilise toujours une notation d'exponentiation ordinaire.

Les notations dans lesquelles une tétration peut être notée (parmi celles permettant même des niveaux d'itérations plus élevés) incluent :

  • la notation standard : ba, utilisée en premier lieu par Hans Maurer; cette notation a été popularisée le livre de Rudy Rucker, Infinity and the Mind.
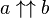
  • la notation des puissances itérées de Knuth : a \uparrow\uparrow b — peut être étendue en utilisant plus de flèches (ou de manière équivalente, une flèche indexée).
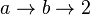
  • la notation des flèches chaînées de Conway : a \rightarrow b \rightarrow 2 — peut être étendue en augmentant le nombre 2 (équivalentes avec les extensions au-dessus), mais aussi, de manière plus performante, en étendant la chaîne.
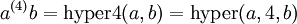
  • la notation hyper4 : a^{(4)}b = \operatorname{hyper4}(a, b) = \operatorname{hyper}(a, 4, b) — peut-être étendue en augmentant le nombre 4; cela donne la famille des hyper opérateurs.

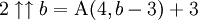
Pour la fonction d'Ackermann, nous avons : 2 \uparrow\uparrow b = \operatorname{A}(4, b - 3) + 3 , i.e. \operatorname{A}(4, n) = 2 \uparrow\uparrow (n+3) - 3 .

La flèche vers le haut est utilisée de manière identique au signe d'omission, ce qui fait que l'opérateur tétration peut être écrit comme ^^ en ASCII : a^^b.

Extension aux valeurs faibles du second opérand

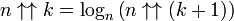
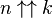
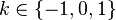
En utilisant la relation n \uparrow\uparrow k = \log_n \left(n \uparrow\uparrow (k+1)\right) (déduite de la définition de la tétration), on peut dériver (ou définir) les valeurs pour n \uparrow\uparrow k pour k \in \{-1, 0, 1\} .

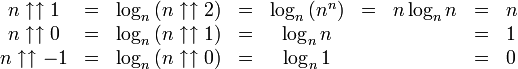
\begin{matrix} n \uparrow\uparrow 1 & = & \log_n \left(n \uparrow\uparrow 2\right) & = & \log_{n} \left(n^n\right) & = & n \log_{n} n & = & n \\ n \uparrow\uparrow 0 & = & \log_{n} \left(n \uparrow\uparrow 1\right) & = & \log_{n} n & & & = & 1 \\ n \uparrow\uparrow -1 & = & \log_{n} \left(n \uparrow\uparrow 0\right) & = & \log_{n} 1 & & & = & 0 \end{matrix}

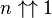
Cela confirme la définition intuitive de n \uparrow\uparrow 1 comme étant simplement n. Cependant, on ne peut plus définir plus de valeurs par itération supplémentaire de cette manière, puisque logn0 est indéfini.

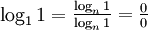
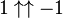
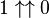
De la même manière, puisque log11 est aussi indéfini ( \log_{1} 1 = \begin{matrix}\frac{\log_n 1}{\log_n 1} = \frac{0}{0}\end{matrix} ), la dérivation au-dessus ne peut être produite lorsque n = 1. Ainsi, 1 \uparrow\uparrow {-1} doit rester une quantité non définie, bien que 1 \uparrow\uparrow {0} puisse être défini sans problème comme étant égal à 1.

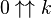
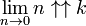
Parfois, 00 est considéré comme quantité indéfinie. Dans ce cas, les valeurs pour 0\uparrow\uparrow{k} ne peuvent être définie directement. Cependant, \lim_{n\rightarrow0} n\uparrow\uparrow{k} est bien défini, et existe :

\lim_{n\rightarrow0} n\uparrow\uparrow k = \begin{cases} 1, & k \mbox{ pair} \\ 0, & k \mbox{ impair} \end{cases}

Cette limite est également valable pour n négatif. 0 \uparrow\uparrow {k} pourrait être définie en termes de cette limite et devrait être en accord avec la définition de 00 = 1 (si 0 est considéré comme pair).

Exemples
- Introduction - Notation - Extension aux valeurs faibles du second opérand - Exemples - Extension aux nombres réels - Tétration complexe - Tours de puissance infiniment hautes
miniature
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
miniature
Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️
miniature
Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜
miniature
Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️
miniature
Cette vitamine développe les fonctions cognitives du cerveau 🧠
miniature
Comment des impacts géants vaporisent les corps planétaires ☄️
miniature
Les Américains riches vivent moins longtemps que les Européens pauvres 💰
miniature
Attention à ce riz naturellement riche en arsenic 🍚
miniature
L'intelligence artificielle contre la mort subite 💀
miniature
L'inévitable formation d'un océan de magma basal sur Terre 🔥
miniature
Découverte d'une plante étrange sans chlorophylle 🌱
miniature
Existe-t-il des mélodies naturelles ? 🎶
miniature
Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽
miniature
L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡
miniature
1
Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺
miniature
Imprimer en 3D avec la lumière du soleil ☀️
miniature
La pollution atmosphérique nuit gravement au cerveau 🧠
miniature
Le trou noir supermassif Ansky vient de se réveiller ⚫
miniature
1
Voici ce qui rend notre cerveau vraiment unique 🧠
miniature
Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩
miniature
Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬
miniature
La physique révèle les secrets d'un strike parfait au bowling 🎳
miniature
Le TDAH associé à la démence 🧠
miniature
Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️
miniature
Le régime cétogène montre des surprises sur le cholestérol 🧐
miniature
Un tango observationnel révèle une Super-Terre 🔭
miniature
Cette expérience montre que la graisse brune augmente fortement la longévité 🕒
miniature
1
L'Univers comme jamais vu auparavant: les révélations du fond diffus cosmologique 🔭
miniature
C'est sérieux: de la bave pourrait révolutionner la conception de bioplastiques 🪱
miniature
Découverte: le trou noir central de notre galaxie pourrait anéantir la vie sur Terre 💥
miniature
Etude scientifique: ces aliments nous font vieillir 🍽️
miniature
Pourquoi notre visage est-il plus petit et délicat que celui des Néandertaliens ? 🤔
miniature
A 18 ans, il découvre 1,5 million d'objets célestes inconnus avec son algorithme d'IA 🌟
miniature
Que sont ces objets rouges et aplatis, qualifiés d'UFOs par les astronomes ? 🔭
miniature
1
Une méthode simple pour améliorer les performances en mathématiques 🧮
miniature
Que sont ces étranges éclairs rouges photographiés au-dessus de l'Himalaya ? ⚡
miniature
Nous descendons non pas d'un, mais d'au moins deux groupes anciens 🧬
miniature
Un nuage géant de 160 000 soleils découvert dans notre Voie lactée 🔭
miniature
Connaissez-vous le rat-kangourou musqué, ce marsupial à la démarche unique ? 🦘
miniature
Comment une poignée de traders a fait s'effondrer deux cryptomonnaies 📉
miniature
Première cartographie titanesque d'un cerveau, avec 500 millions de connexions neuronales 🧠
miniature
Cette double supernovae proche est inexorable, voici la date... qui va vous surprendre 💥
miniature
Un océan phosphorescent: comment s'explique ce phénomène rare et féerique ? 🌊
miniature
L'ELT pourrait-il découvrir une vie extraterrestre dès 2028 ? 🔭
miniature
Cet édulcorant tue les superbactéries résistantes 🍬
miniature
Les neutrinos, la clé de la gravité quantique ? 👀
miniature
En Italie, les éruptions explosives de ce volcan déjouent les pronostics 🌋
miniature
Que sont ces spaghettis au cœur de notre galaxie ? 🔭
miniature
Des scientifiques ont créé une "bombe intelligente" contre le cancer 🎯
Page générée en 0.101 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise