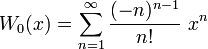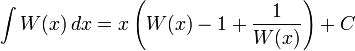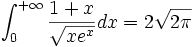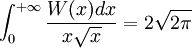Fonction W de Lambert - Définition
La fonction W de Lambert, nommée ainsi par Johann Heinrich Lambert, est aussi appelée la fonction Oméga, et est la fonction réciproque de f définie par :
- pour tout nombre complexe w, f(w) = w e w.
Ce qui implique que pour tout nombre complexe z, nous avons :
- W(z) eW(z) = z
Puisque la fonction f n'est pas injective, la fonction W est multiforme.
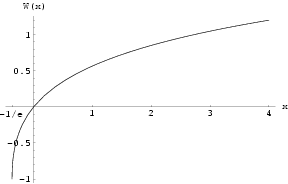
Si nous nous limitons aux arguments réels x ≥ -1/e (ce qui exige w ≥ -1) alors il existe une fonction et une seule W0 définie, dont la représentation graphique figure ci-dessous.
Les valeurs remarquables sont :
- W0(0) = 0
- W0(-1/e) = -1
- W0(1) = Ω
La fonction W de Lambert ne peut pas être exprimée à l'aide de fonctions élémentaires. Elle est utile en combinatoire, par exemple dans l'énumération des arbres. Elle peut être utilisée pour résoudre diverses équations qui comportent des exponentielles et apparaît aussi dans les solutions d'équations différentielles à temps-retardés, telles que y'(t) = a y(t - 1).
Par différenciation, on peut montrer que W satisfait l'équation différentielle :
- pour z ≠ -1/e, z (1 + W) dW/dz = W .
La série de Taylor de W0 au voisinage de 0 peut être obtenue par l'utilisation du théorème d'inversion de Lagrange et est donné par
Le rayon de convergence est égal à 1/e. Celle-ci peut être prolongée en une fonction holomorphe définie en tout nombre complexe n'appartenant pas à l'intervalle réel ]-∞, -1/e]; cette fonction holomorphe est aussi appelée la branche principale de la fonction Lambert W.
Beaucoup d'équations impliquant des exponentielles peuvent être résolues par l'utilisation de la fonction W. La stratégie générale est de déplacer toutes les instances de l'inconnue d'un côté de l'équation et de le faire ressembler à x e x. À ce point la fonction W nous fournit la solution. Par exemple, pour résoudre l'équation 2t = 5t, nous divisons par 2 t pour obtenir 1 = 5t e-ln(2)t, nous divisons alors par 5 et multiplions par -ln(2) pour obtenir -ln(2)/5 = -ln(2)t e-ln(2)t. Maintenant l'application de la fonction W donne -ln(2)t = W(-ln(2)/5), i.e. t = -W(-ln(2)/5) /ln(2).
La fonction W, et beaucoup de fonctions impliquant W, peuvent être intégrées en utilisant le changement de variable w = W(x), i.e. x = w ew:
Diverses formules
-
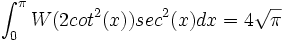
Conséquences :