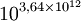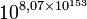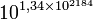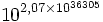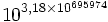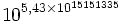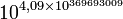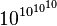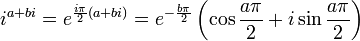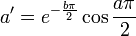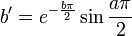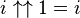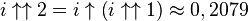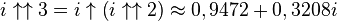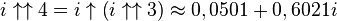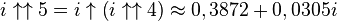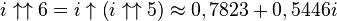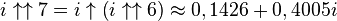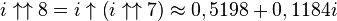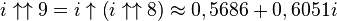Tétration - Définition

Exemples

(Les exemples avec virgules sont approchées)

n = n↑↑1	n↑↑2	n↑↑3	n↑↑4
1	1	1	1
2	4	16	65 536
3	27	7,63×1012
4	256	1,34×10154
5	3 125	1,91×102 184
6	46 656	2,70×1036 305
7	823 543	3,76×10695 974
8	16 777 216	6,01×1015 151 335
9	387 420 489	4,28×10369 693 099
10	10 000 000 000	1010 000 000 000

Extension aux nombres réels

L'extension de aux nombres réels x > 0 est relativement simple et donne, pour chaque nombre naturel b, une fonction super-puissance (le préfixe super est parfois remplacé par hyper : fonction hyper-puissance).

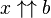
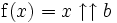
Comme indiqué précédemment, pour les entiers positifs b, la fonction tends vers 1 pour x tendant vers 0 si b est pair, et vers 0 si b est impair, alors que pour b = 0 et b = − 1, la fonction est constante, avec pour valeur 1 et 0, respectivement.

À ce jour, il n'existe pas de solution communément acceptée pour le problème général d'extension de la tétration aux nombres réels et complexes, bien que cela soit un champ de recherche actif.

Considérons le problème de trouver une fonction super-exponentielle ou une fonction hyper-exponentielle qui est une extension au réel x > − 2 de ce qui est défini précédemment, et qui satisfait (pour a > 1) :

• .
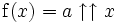
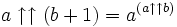
• une croissance monotone.
• une condition de continuité.

Lorsque est définie comme un intervalle de longueur unitaire, la fonction dans son ensemble convient facilement pour tout x > − 2.

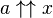
Une solution simple est donnée par pour − 1 < x < 0, par conséquent pour 0 < x < 1, pour 1 < x < 2, etc.

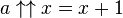
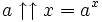
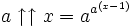
Cependant, elle est différentiable par parties, à des valeurs entières de x, la dérivée est multipliée par log_na: , , .

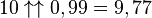
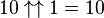
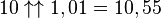
D'autres fonctions, plus compliquées, peuvent être plus douces et/ou satisfont des propriétés additionnelles.

Une fonction super-exponentielle croît plus vite qu'une fonction double exponentielle; par exemple, si a = 10:

• 
• 
• 
• 
• (googol)
• 
• (googolplex)
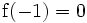
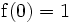
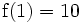
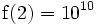
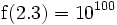
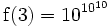
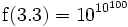
• Cela devient pour x = 2,376:

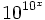
Lorsque l'on définit pour tout a, une autre condition requise peut être que est croissante monotone avec a.

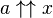
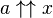
Ces fonctions inverses sont appelées super-racines ou hyper-racines, et super-logarithme ou hyper-logarithme slog_a définie pour tous les nombres réels, y compris les nombres négatifs.

La fonction slog_a satisfait à :

slog_aa^b = 1 + slog_ab

slog_ab = 1 + slog_alog_ab

slog_ab > − 2

Exemples:

• slog₁₀ − 3 = − 1 + slog₁₀0,001 = − 1 + − 0,999 = − 1,999
• slog₁₀3 = log₁₀3 = 0,477
• 

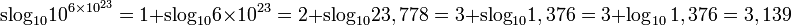
Tétration complexe

Puisqu'un nombre complexe peut être élevé à la puissance, la tétration peut être appliquée aux nombres de la forme a + bi, dans lesquels i est la racine carrée de -1. Ainsi par exemple, dans lequel n = i, la tétration est effectuée en utilisant la branche principale du logarithme naturel, et on a la relation :

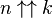
Ce qui suggère une définition récursive pour pour tout :

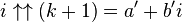
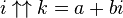
Les valeurs approximées suivantes peuvent en être déduites, pour lesquelles est l'exponentiation ordinaire (i.e. iⁿ).

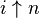
La résolution de la relation conduit aux relations attendues et , avec des valeurs négatives de k donnant des résultats infinis sur les axes imaginaires. Dans le plan complexe, la séquence entière converge en spirale vers la limite 0,4383 + 0,3606i, ce qui peut être interprété comme la valeur pour laquelle k est infini.

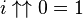
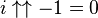
De telles séquences de tétration ont été étudiées depuis l'époque d'Euler mais sont très peu comprises en raison de leur comportement chaotique. Les recherches les plus publiées se sont historiquement concentrées sur la convergence de la fonction de tour de puissance. La recherche actuelle a grandement bénéficié du progrès de puissantes stations de calcul avec des supports logiciel en mathématiques symboliques et fractales. La plupart de ce qui est connu sur la tétration vient de la connaissance générale de la dynamique complexe et de la recherche spécifique sur les nappes exponentielles.