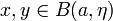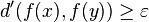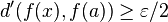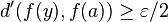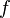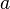Théorème de Heine - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le théorème de Heine, nommé ainsi en l'honneur de Édouard Heine, s'énonce ainsi : toute application continue d'un espace métrique compact dans un espace métrique quelconque est uniformément continue. Cela implique notamment que toute fonction continue d'un segment [a,b] dans

Énoncé et démonstration pour les fonctions numériques
Énoncé
Théorème — Soit une fonction
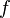
![[a,b]~](https://static.techno-science.net/illustration/Definitions/autres/a/ac5c11f7d0581018532328d92f207e1e_4bd88211be7f129defe6bae1bf0d41fb.png)

![[a,b]~](https://static.techno-science.net/illustration/Definitions/autres/a/ac5c11f7d0581018532328d92f207e1e_4bd88211be7f129defe6bae1bf0d41fb.png)
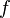
Utilisation
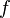
![\forall x \in [a,b], \forall \varepsilon > 0, \exists \alpha_{x,\varepsilon} > 0](https://upload.wikimedia.org/math/2/d/a/2da3e48713f48442633bdfbfa27238eb.png) tel que
tel que
![\forall y \in [a,b], |x-y|<\alpha_{x,\varepsilon} \Rightarrow |f(x)-f(y)|<\varepsilon](https://static.techno-science.net/illustration/Definitions/autres/2/2f32a03af9c79192e4ad0a0c5c87ef2a_91b1806cdbcb9a444e5c3621596edee0.png)
Le théorème de Heine permet donc d'affirmer qu'elle est uniformément continue sur le segment
![[a,b]~](https://static.techno-science.net/illustration/Definitions/autres/a/ac5c11f7d0581018532328d92f207e1e_4bd88211be7f129defe6bae1bf0d41fb.png)
![\forall x \in [a,b], \exists \alpha_x](https://static.techno-science.net/illustration/Definitions/autres/c/c6c201d426d6bb94550a4d8c3fd62e5e_9a4972a16e88a843ca3b1bac35a312e0.png)
![\exists \alpha, \forall x \in [a,b]](https://static.techno-science.net/illustration/Definitions/autres/b/b97ca2007f9c8899bb608b1dcaeafdd7_e327067a6ccd5196107d156f5ae75ca0.png)
La propriété d'uniforme continuité s'exprime alors :
Propriété —  tel que
tel que
![\forall x \in [a,b], \forall y \in [a,b], |x-y|<\alpha_\varepsilon \Rightarrow |f(x)-f(y)|<\varepsilon](https://static.techno-science.net/illustration/Definitions/autres/5/58dc471bb45b1973ce81d354d848dfc9_843ba30f08b06a5ad80f77e5a9ac44ce.png)
Démonstration
Fixons un  et posons, pour tout
et posons, pour tout
![x\in[a,b]](https://static.techno-science.net/illustration/Definitions/autres/8/8290bddba5acf9822dcbf61f4ac67d1b_92fce6cd0dff07f919fd3d074608a860.png)
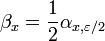
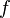
Considérons
![[a,b]=\cup_{x\in[a,b]} \{x\} \subset \cup_{x\in[a,b]} B(x,\beta_x)](https://static.techno-science.net/illustration/Definitions/autres/4/448083f6d93d46b4a2df875090edb80a_15ce2cea37613aaf51cbf9adb4288fa9.png)
![[a,b]~](https://static.techno-science.net/illustration/Definitions/autres/a/ac5c11f7d0581018532328d92f207e1e_4bd88211be7f129defe6bae1bf0d41fb.png)
![[a,b]\subset\cup_{z\in Z}B(z,\beta_z)](https://static.techno-science.net/illustration/Definitions/autres/e/e20cd313a6913c3320261cb8890cbc10_aa395edae38cf93b2fdb64fa2ca1ee8b.png)
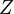
![[a,b]~](https://static.techno-science.net/illustration/Definitions/autres/a/ac5c11f7d0581018532328d92f207e1e_4bd88211be7f129defe6bae1bf0d41fb.png)
Posons
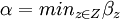
![x,y\in[a,b]](https://static.techno-science.net/illustration/Definitions/autres/c/cb79e328f847e7458950b6147a06dbba_c2429901792449daa95c5fb13cea03f7.png)
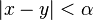
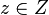
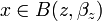
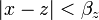
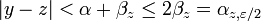
Donc :
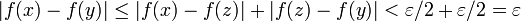
La valeur α trouvée étant bien indépendante de
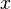
Énoncé et démonstrations dans le cas général
Énoncé
Théorème — Soient X un espace métrique compact, Y un espace métrique, et
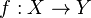

On note
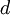
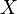
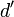
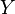
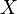
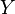
 tel que
tel que
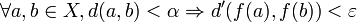
Démonstration directe
On peut reproduire la démonstration précédente en remplaçant simplement
![[a,b]~](https://static.techno-science.net/illustration/Definitions/autres/a/ac5c11f7d0581018532328d92f207e1e_4bd88211be7f129defe6bae1bf0d41fb.png)
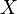

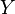
Démonstration par la propriété de Bolzano-Weierstrass
Une autre méthode est de raisonner par contraposée en supposant
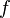
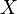
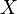
 tel que pour chaque
tel que pour chaque  , l'implication
, l'implication
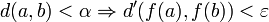
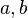
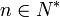
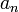
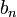
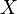
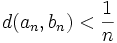
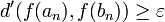
La suite
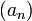
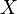
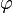
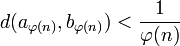
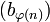
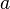
 , il existe
, il existe