Démonstration directe - Définition
Dans une démonstration directe, pour montrer que
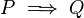
Ce type de raisonnement s'oppose au raisonnement par contraposition, dans lequel on part de l'hypothèse que Q est fausse, et où on cherche à montrer que dans ce cas P doit être fausse elle aussi.
Exemple
On cherche à montrer que si n est impair alors n2 est impair.
On pose donc donc P : " l'entier n est impair " et Q : " l'entier n2 est impair ".
On prend l'hypothèse que P est vraie et on veut montrer que Q doit être vraie.
n est impair, donc ceci implique (définition d'impair) que n = 2k + 1 où k appartient à

Alors, n2 = (2k + 1)(2k + 1) = 4k2 + 4k + 1 = 2(2k2 + 2k) + 1 = 2t + 1 où t = 2k2 + 2k est un entier.
Conclusion : 2t + 1 est impair donc n2 est impair.

















































