Continuité - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, la continuité est une propriété topologique d'une fonction. En première approche, une fonction est continue si, à des variations infinitésimales de la variable x, correspondent des variations infinitésimales de la valeur f(x).
La continuité est associée à la notion de continuum dont l'origine est géométrique. Dans un continuum géométrique, comme le plan ou l'espace, un point peut se déplacer continument pour s'approcher à une précision arbitraire d'un autre point. La notion de continuité est définie de manière rigoureuse en mathématiques.
Le premier exemple de fonctions continues concerne des fonctions réelles définies sur un intervalle et dont le graphe peut se tracer sans lever le crayon. Cette première approche donne une idée de la notion (la fonction ne saute pas) mais n'est pas suffisante pour la définir, d'autant plus que certains graphes de fonctions pourtant continues ne peuvent pas se tracer de cette manière, telle par exemple la fractale.
Historiquement définie pour des fonctions de la variable réelle, la notion de continuité se généralise à des fonctions entre espaces métriques ou entre espaces topologiques sous une forme locale et sous une forme globale.
L'étude des fonctions continues se révèle fructueuse pour les propriétés qu'elles possèdent (propriété de convergence, théorème des valeurs intermédiaires, théorème des bornes, application lipschitzienne, intégrabilité).
Définition pour les fonctions réelles
Définition — Soient I un intervalle réel,
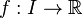
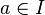
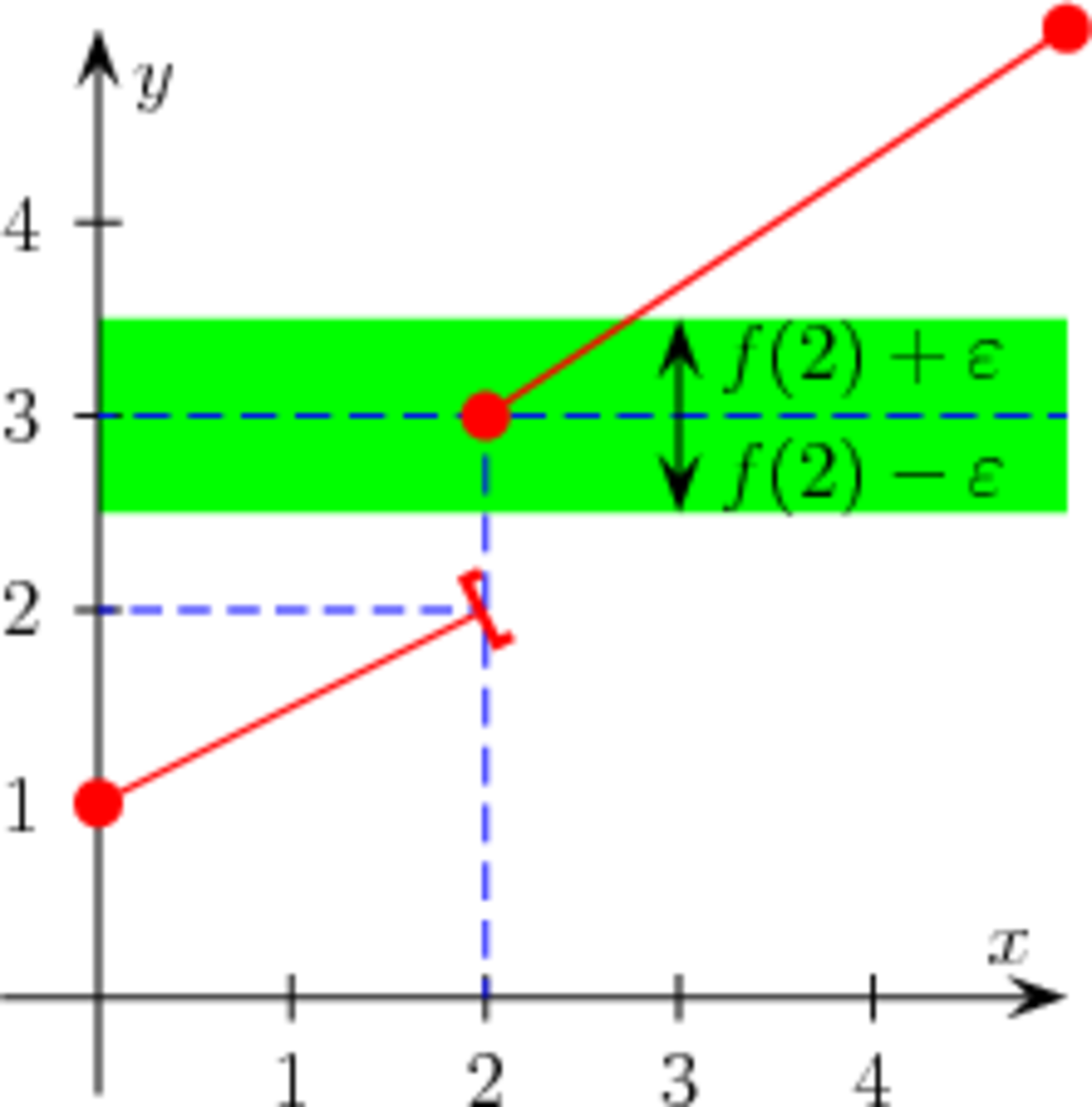
La fonction f est dite continue en a si :
Ainsi f est continue en a si et seulement si la limite de f en a existe et vaut f(a).
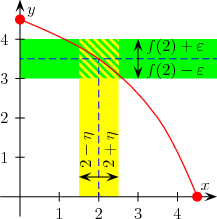
Cela veut dire que si l'on se fixe un seuil ε, on peut trouver un intervalle autour de a tel que ƒ(x) soit à une distance inférieure à ε de ƒ(a).
- Si la continuité est valable uniquement à droite (pour x>a), on dit que f est continue à droite en a. De même à gauche pour a.
Dire que f est continue en a revient à dire qu'elle l'est à droite et à gauche en a.
- La fonction ƒ est dite continue (sur I) si elle est continue en tout point a de I.
Une fonction qui présente des « sauts » est discontinue. La notion de saut est illustrée sur la figure ci-contre, elle correspond à l'existence d'une limite à droite et d'une limite à gauche qui ne valent pas la même chose.
Commentaire
C'est l'idée du seuil, ε, fixé à l'avance qui est importante. Cette définition, fruit des efforts des mathématiciens du XIXe siècle pour rendre rigoureuse la notion intuitive de continuité, peut sembler à bon droit violente. En analyse non standard, une approche plus intuitive est possible : on dira que f est continue en

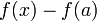
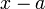
La définition globale de la continuité dans le cadre des espaces topologiques(voir plus bas) permet elle aussi de se débarrasser des

Exemples
- Une grande partie des fonctions usuelles sont continues sur leur intervalle de définition : fonctions polynômes, rationnelles, exponentielles, logarithmes, hyperboliques, trigonométriques, racine carrée, racine cubique, valeur absolue.
- La fonction carré :
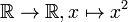
- La fonction partie entière sur les réels est discontinue : on « lève le crayon » en arrivant à chaque entier.
- Une fonction réelle dérivable en un point est continue en ce point. Par contre la réciproque est fausse (par exemple la fonction racine carrée est continue en 0, mais n'y est pas dérivable, tout comme la fonction valeur absolue continue en 0 mais non dérivable en ce point).
- Une fonction réelle peut n'être continue en aucun point : c'est le cas de
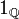

Propriétés
La notion de continuité sur un intervalle pour les fonctions réelles
- est utile pour prouver l'existence de solutions à des équations de la forme f(x) = m (voir théorème des valeurs intermédiaires)
- simplifie le calcul de limites car
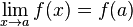
La composée de fonctions continues est une fonction continue. La composée d'une fonction continue et d'une suite convergente est une suite convergente.
Les propriétés de stabilité de la continuité par combinaison linéaire (i.e. pour tous α, β réels et f, g fonctions réelles continues, on a que α.f + β.g est continue) et par produit de deux fonctions font de l'ensemble des fonctions continues une algèbre sur le corps des réels.
Des erreurs à éviter
- Une fonction dérivable en un point est continue sur ce point, la réciproque est fausse.
- Contre exemple : la fonction
![f(x)=\sqrt[]{x}](https://static.techno-science.net/illustration/Definitions/autres/f/f0fbd2552c18a6c752e875ec4fa5cb6b_2ff61a51283620e87a75dffcd383d2d4.png)
- Contrairement à ce qui en est parfois dit, des fonctions telles que
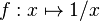
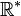
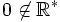

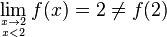

![\forall \varepsilon > 0 \quad \exists \eta > 0 \quad \forall x \in I \quad \Big[|x - a| \leq \eta \implies |f(x) - f(a)| \leq \varepsilon\Big]](https://upload.wikimedia.org/math/2/0/e/20eefb8e8625f5bb6dec27952fc8237f.png)

















































