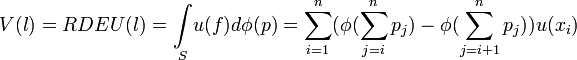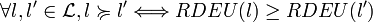Théorie de la décision - Définition
La liste des auteurs de cet article est disponible ici.
La théorie de la décision dans le risque
Optimisation et maximalisation sont les deux mots-clés définissant les théories de la prise de décision basées sur la rationalisation, c’est-à-dire les théories définissant les normes logiques et rationnelles que tous les preneurs de décisions sont censés suivre pour que le choix soit celui qui "rapporte" le plus. La théorie de l'utilité espérée est l'approche la plus communément retenue par la théorie de la décision pour décrire les choix risqués. Introduisons d'abord quelques notations:
L'incertitude est décrite par un ensemble d'états du monde
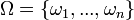
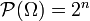
Un élément de
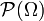
Une variable aléatoire f est une fonction qui associe à chaque ω un résultat noté x.
L'ensemble des résultats est noté X, X étant un sous-ensemble de
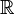
On écrit
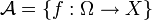
Dans le cas du risque, le décideur est supposé connaître les distributions de probabilités induites par les variables aléatoires. La distribution induite par la variable aléatoire f est notée lf. La relation binaire

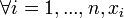
![\mathcal{L}=\left\{ l_{f}:X\rightarrow\left[0;1\right]\mid{\textstyle f\in\mathcal{A}},\sum_{i=1}^{i=n}l_{f}(x_{i})=1\right\}](https://static.techno-science.net/illustration/Definitions/autres/5/5366383c6eca481b1d1d9cdee841e087_0b6b961b0cfa926e8d8997b506f67380.png)

Axiome 1 (préordre total).

-
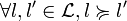
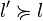
-
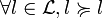
-
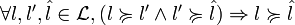
Axiome 2 (Monotonie).

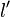
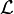
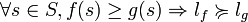
Axiome 3 (Continuité).

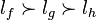
![\exists \alpha,\beta\in\left]0;1\right[](https://static.techno-science.net/illustration/Definitions/autres/0/0dc41c67717aa02526e6f63556060d4b_241c244e30c1d81dbb04753d46cd940e.png)
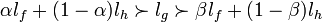
Axiome 4 (Indépendance).

![\left[0;1\right]](https://static.techno-science.net/illustration/Definitions/autres/a/a4ad45521d55891c0df40fc4615333a1_a1ceff39ed56a9271e9b6cac7cc5502e.png)
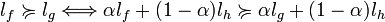
Nous pouvons maintenant présenter le théorème de représentation de Von Neumann et Morgenstern :
Théorème. Pour une loterie l = (x1,p1;...;xn,pn), on définit la fonction espérance-utilité par
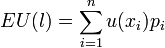

(i)

(ii) Il existe une fonction à valeurs réelles

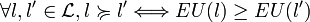
Le contenu descriptif du modèle de décision EU a été rapidement critiqué dans une expérience restée cèlèbre sous le nom de "paradoxe d'Allais". La version présentée ici est celle de Kahneman et Tversky (1979). Les sujets doivent choisir entre deux paires de loteries. D'une part, entre l1 = (3000,1) et l2 = (0,0.2;4000,0.8) et, d'autre part, entre l3 = (0,0.75;3000,0.25) et l4 = (0,0.8;4000,0.2). Le choix le plus fréquemment observé est l1 dans la première paire et l4 dans la seconde paire, en contradiction avec les prédictions de la fonction EU(.). Plus spécifiquement, c'est l'axiome d'indépendance qui est violé par les individus. Pour résoudre ce paradoxe, une réponse courante consiste à supposer que le traitement des probabilités n'est pas linéaire. Les individus "déforment" les probabilités en fonction des résultats (par exemple, ils sous-estiment la probabilité d'obtenir 3000 dans la loterie l3). Principalement axiomatisé par Quiggin (1982), le modèle suivant, appelé "Rank-Dependent Expected Utility " (RDEU), repose principalement sur un affaiblissement de l'axiome d'indépendance. Celui-ci ne tient plus que sur les distributions de probabilités induites par les variables aléatoires ayant le même tableau de variation, c'est-à-dire qui sont communément monotones, ou encore comonotones :
Axiome 4' (Indépendance comonotone).

![\left[0;1\right]](https://static.techno-science.net/illustration/Definitions/autres/a/a4ad45521d55891c0df40fc4615333a1_a1ceff39ed56a9271e9b6cac7cc5502e.png)
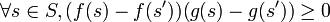
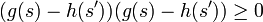
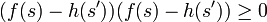
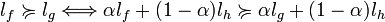
Théorème. Etant donnée une relation de préférences



![\phi:\left[0;1\right]\rightarrow\left[0;1\right]](https://static.techno-science.net/illustration/Definitions/autres/c/c29d9b08acdf31825f8c597027366479_6f927900bfbfbe1e3582722e0bb4fe72.png)