Relation binaire - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une relation binaire sur un ensemble E, ou tout simplement relation sur un ensemble E est caractérisée par une collection de couples d'éléments de E, en d'autres termes un sous-ensemble du produit cartésien E × E, que l'on appelle son graphe. Les composantes d'un couple appartenant au graphe d'une relation R sont dit en relation par R. L'égalité entre éléments d'un ensemble E est un exemple de relation sur E. La relation « ... est strictement inférieur à ... », notée « < », sur l'ensemble N des nombres entiers est une relation sur N. On note n < p pour indiquer que n et p sont en relation. Le couple (0,1) est un élément du graphe de cette relation.
Plus généralement une relation entre deux ensembles E et F est aussi appelée relation binaire. Elle est définie par son graphe, une collection de couples dont la première composante est dans E et la seconde dans F, c'est-à-dire un sous-ensemble du produit cartésien E × F. Un exemple en est, en géométrie plane, la relation d'incidence — être sur — entre un point et une droite du plan: « le point A est sur la droite D » . C'est une relation binaire entre l'ensemble des points du plan et l'ensemble des droites du plan. Les fonctions ou applications d'un ensemble E dans un ensemble F peuvent être vues comme des cas particuliers de relations binaires entre E et F. Une relation binaire entre deux ensembles est aussi appelée parfois correspondance entre ces deux ensembles.
On parle aussi de relation pour des notions plus générales, en particulier on peut définir des relations à plus de deux arguments, voir relation (mathématiques).
Introduction
De manière informelle, une relation entre deux ensembles est une proposition qui lie certains éléments du premier ensemble avec d’autres éléments du second ensemble.
Sur un ensemble F constitué de filles et un ensemble G constitué de garçons, par exemple, on pourrait définir une relation « Alice aime Bernard », ou une autre relation « Béatrice connaît Paul »... On peut donc voir la relation comme étant des fils reliant des éléments de deux ensembles.
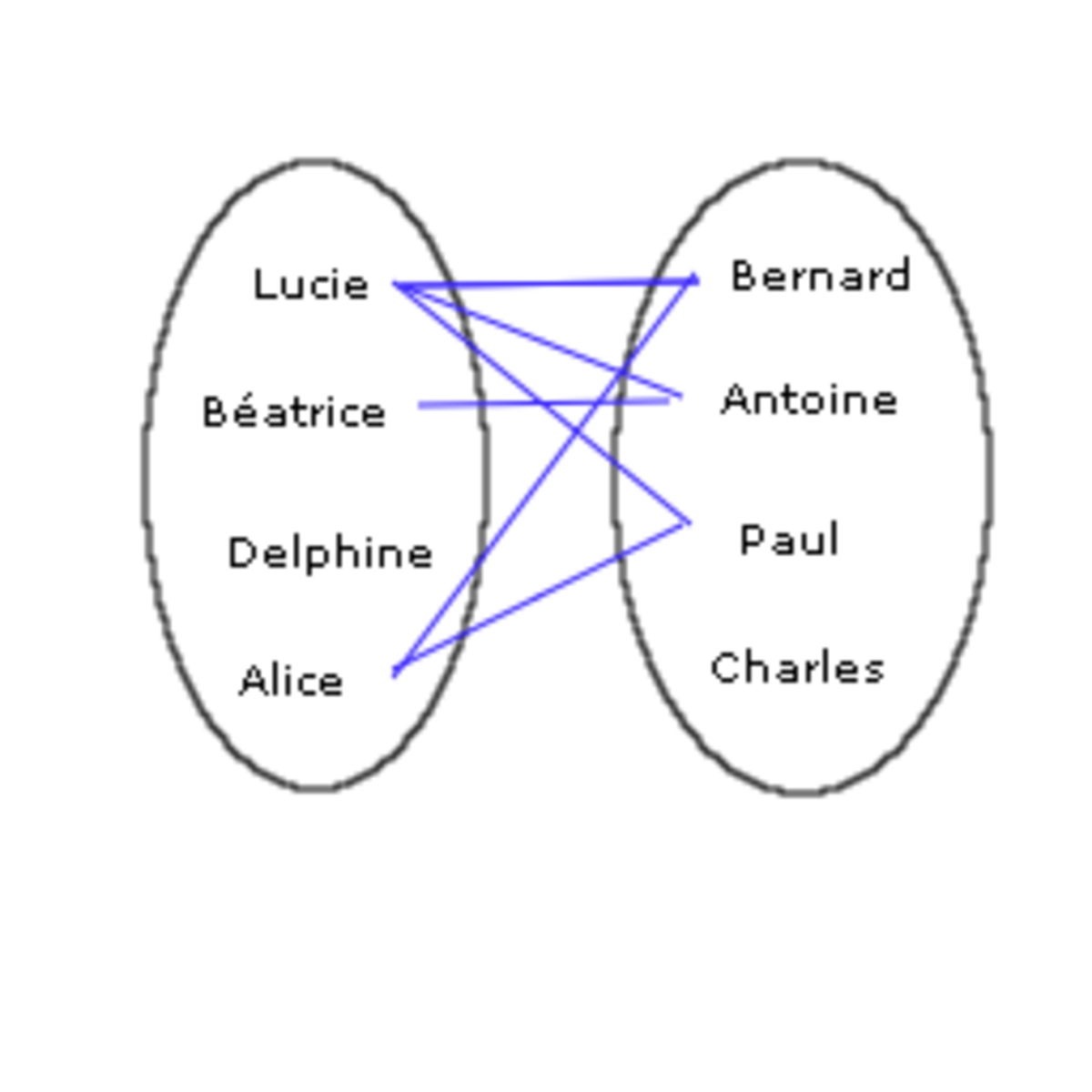
Dans le cas d’un ensemble fini, on peut alors tenter de représenter la relation par un diagramme. Si F = {Lucie, Béatrice, Delphine, Alice} et si G = {Bernard, Antoine, Paul, Charles}, la relation aime peut être schématisée par le diagramme joint (un tel diagramme est dit diagramme sagittal).
On peut également représenter cette relation, par un tableau à deux entrées, avec en première colonne la liste des éléments de l’ensemble de départ F, et en première ligne celle des éléments de l’ensemble d’arrivée G. Les couples sont représentés par des croix dans les cases à l’intersection de la ligne de la première composante et de la colonne de la seconde composante.
| . | Bernard | Antoine | Paul | Charles |
|---|---|---|---|---|
| Lucie | X | X | X | . |
| Béatrice | . | X | . | . |
| Delphine | . | . | . | . |
| Alice | X | . | X | . |
On pourra déplorer le fait que Delphine n’aime personne, que Lucie ait un cœur généreux et que Charles puisse se sentir seul.
On peut aussi tenter de faire la liste des couples ainsi en relation (pour plus de commodité, on ne conservera que les deux premières lettres du prénom):
- Gr = {(Lu,Be) , (Lu, An) , (Lu, Pa) , (Bé, An) , (Al, Pa) , (Al, Be)}
En mathématique, un « couple » est formé de deux éléments mis entre parenthèses dans un ordre particulier. La relation est définie en première approche comme un ensemble de couples, c’est-à-dire que si deux éléments sont reliés entre eux, alors le couple est un élément de l’ensemble relation. Si l’on appelle F l’ensemble des filles, et G l’ensemble des garçons, alors l’ensemble de tous les couples possibles est appelé « produit cartésien de F par G » et est noté F×G et la relation aime est alors définie par l’ensemble F, l’ensemble G et un sous-ensemble de F×G.