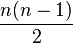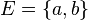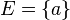Paire - Définition

Introduction

On dit qu'un ensemble E est une paire lorsqu'il est formé de deux éléments distincts a et b, et il s'écrit alors :

Quand l'ensemble E est formé d'un seul élément, a, on dit que E est un singleton, et on l'écrit alors :

Remarques

• On peut utiliser la notation {a, b} même si a = b. C'est bien utile quand on manipule des variables, on peut écrire {x, y}, sans supposer que x ≠ y, et cela évite de multiplier les sous-cas dans un certain nombre de raisonnements élémentaires de théorie des ensembles. Cependant si a = b alors l'ensemble {a, b} n'est pas une paire mais le singleton {a}.
• La paire est un ensemble : elle n'est pas ordonnée. On peut indifféremment écrire {a, b} ou {b, a} pour désigner le même ensemble. Ceci différencie la paire du couple.

{a, b} = {b, a}, que a et b soient ou non distincts, tandis que (a , b) ≠ (b , a) dès que a et b sont distincts.

Propriétés

Appartenance d'un élément à une paire (ou à un singleton)

On a vu que l'écriture {a, b} peut s'utiliser même si a = b. Nous parlerons donc de paire ou singleton {a, b}.

Un élément x appartient à une paire si et seulement s'il est égal à l'un des deux éléments de cette paire. Cet énoncé est en fait tout autant valable pour un singleton. On peut donc l'écrire formellement, pour a et b donnés :

∀x[ x ∈ {a, b} ⇔ (x = a ou x = b)]

(le « ou » en question désigne, comme d'habitude en mathématiques, une disjonction inclusive : l'énoncé reste vrai si x = a et x = b).

Cette propriété caractérise les paires (ou singletons). Quand on axiomatise la théorie des ensembles, usuellement on utilise un axiome spécifique, appelé axiome de la paire, pour l'existence d'un ensemble ayant cette propriété, deux éléments non nécessairement distincts étant donnés.

Dans le cas des singletons (a = b), la propriété caractéristique peut bien-sûr se simplifier :

∀x[ x ∈ {a} ⇔ x = a].

Égalité de deux paires (ou singletons)

Deux paires ou singletons sont égales si et seulement si leurs éléments sont égaux deux à deux, de l'une des deux façons dont on peut les associer. Plus précisément, pour deux paires ou singletons {a, b} et {c, d} :

[{a, b} = {c, d}] ⇔ [(a = c et b = d) ou (a = d et b = c)]

L'énoncé se simplifie si l'on sait que l'une des deux ensembles est un singleton :

[{a} = {c, d}] ⇔ [a = c et a = d]

et se simplifie d'autant plus pour l'égalité des singletons :

{a} = {c} ⇔ a = c

Paires disjointes

Deux paires ou singletons sont disjointes si et seulement si chacun des éléments de la première paire ou singleton sont distincts de chacun des deux éléments de l'autre, ce qui, pour des paires, signifie que les quatre éléments des deux paires sont deux à deux distincts. Pour deux paires ou singletons {a, b} et {c, d} on a donc :

{a, b} ∩ {c, d} = ∅ si et seulement si (a ≠ c et a ≠ d et b ≠ c et b ≠ d)

Cardinalité d'une paire

La cardinal d'un ensemble est ce l'on appelle usuellement pour les ensembles finis son nombre d'éléments. Une paire est donc évidemment un ensemble fini de cardinal 2.

Autres propriétés

• Un raisonnement simple de dénombrement montre que le nombre de paires (les « vraies » paires, sans les singletons) d'un ensemble fini à n éléments est égal à (voir l'article combinaison).