Théorie de la décision - Définition

Introduction

La théorie de la décision est une théorie de mathématiques appliquées ayant pour objet la prise de décision en univers risqué.

Les limites de la théorie des probabilités

En présences de choix, la théorie des probabilités propose de calculer les espérances mathématiques de gain et d'opter pour le choix qui maximise cette espérance de gain. Cependant ce procédé a plusieurs limites. La théorie de la décision vise à apporter une réponse à ces cas limites.

Gain non quantifiable

D'autre part, dans de nombreux cas, les gains ne sont pas quantifiables (voir l'exemple du pari de Pascal, ou de l'assurance vie), difficilement mesurables (comme les catastrophes) ou difficilement comparables. Là encore, la théorie de la décision cherche à apporter des réponses, à établir des préférences.

Risque ou incertitude ?

En théorie de la décision, on distingue le risque de l'incertitude. Le risque désigne une situation dans laquelle les distributions de probabilités sur les résultats existent et sont connues des agents : c'est par exemple le cas du loto ou d'un lancer de dés. L'attitude vis-à-vis du risque d'un décideur est cruciale pour comprendre son comportement face à des situations risquées. Considérons le choix de participer à un jeu où le joueur a une chance sur dix de gagner cent fois sa mise. L'espérance de gain est très positive et tout joueur serait prêt à miser 1 euro ; mais qui ferait le choix de jouer si la mise obligatoire était toute la fortune du joueur ? Dans le premier cas, on parlera d'aversion pour le risque et dans le second cas, de préférence pour le risque. Le comportement normal est une certaine aversion au risque.

Si les situations de risque constituent, dans la vie courante, des situations assez marginales, l'incertitude est en revanche omniprésente. Elle désigne les situations dans lesquelles les distributions de probabilités n'existent pas ou ne sont pas connues des agents. C'est par exemple le cas d'une course de chevaux : sur quel cheval parier sachant que l'on ne connaît pas la probabilité qu'a chaque cheval de gagner ? La théorie de la décision est également capable d'apporter des réponses à ce type de situation.

La théorie de la décision dans l'incertain

L'utilité espérée a été élargie dès 1954 par L.J. Savage aux situations incertaines. Son axiomatisation comporte six axiomes lorsque l'ensemble Ω est fini. Un axiome "clé" est le suivant :

Axiome (Principe de la chose sûre). est telle que pour tout événement E et actes et tels que et , et et , si et seulement si .

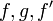
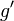
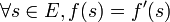
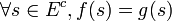
En addition aux hypothèses "standards" (préordre complet, monotonie, continuité), cet axiome permet à la relation de préférences d'être représentée par une fonction SEU(.) tel que où :

• La fonction est affine à une transformation affine croissante près ;
• La fonction d'ensemble est une mesure de probabilité ;
• SEU signifie "Subjective Expected Utility", l'adjetif "subjective" étant là pour rappeler que la mesure P(.) est attribuée par le décideur et n'est pas une donnée objective du problème de décision.

Bien que séduisant par sa simplicité et sa relative souplesse d'utilisation comparée à d'autres approches, le modèle de l'utilité espérée dans l'incertain a fait l'objet de plusieurs critiques expérimentales. La principale est liée au principe de la chose sûre, qui neutralise l'impact de l'ambiguïté sur les préférences, comme le suggère l'exemple suivant, qui constitue une variante du paradoxe d'Ellsberg (1961).

Exemple(Paradoxe d'Ellsberg). Un individu est face à une urne contenant 30 boules rouges, et 60 boules bleues ou vertes, sans information supplémentaire sur le nombre exact de boules vertes d'une part, de boules bleues d'autre part. La probabilité d'obtenir une boule rouge, notée P(R) ,est donc connue et égale à , de même que celle d'obtenir une boule qui serait soit bleue, soit verte : . Cependant, il ne s'agit pas d'une situation de risque puisque la probabilité d'obtenir une boule bleue, P(B), varie dans l'intervalle , tout comme celle d'obtenir une boule verte, P(V). Nous parlons d'ambiguïté pour qualifier une telle situation, dans laquelle seulement une partie de l'information est probabilisée. Supposons que l'individu doive effectuer un choix entre les actes suivants :

• a=(1 si R, 0 si B, 0 si V) contre a'=(0 si R, 1 si B, 0 si V)
• b=(1 si R, 0 si B, 1 si V) contre b'=(0, si R, 1 si B, 1 si V)

Dans le choix "a contre a'", on observe généralement , tandis que dans le choix "b contre b'", on observe . L'aversion pour ambiguïté des individus explique ce type de choix. Le premier choix s'explique par le fait que l'individu connaît la probabilité que la boule soit rouge, et le second par le fait qu'il connaît la probabilité qu'elle soit bleue ou verte (mais pas celle qu'elle soit rouge ou verte). Il s'agit d'une contradiction directe du principe de la chose sûre. Par conséquent, de telles préférences ne peuvent être décrites par le critère de l'utilité espérée. En effet, supposons que ce soit le cas. Nous avons donc si et seulement si et si et seulement si P(B) + P(V) > P(R) + P(V). Il s'agit clairement d'une contradiction, raison pour laquelle ce type d'expérience a été qualifié de paradoxe.

D'autres modèles, appelées "Non-Expected Utility" modèles, ou modèles non-additifs, ont donc été axiomatisés dans l'incertain pour résoudre ce type de paradoxe.