Cercle d'Euler - Définition
En géométrie, le cercle d'Euler d'un triangle est le cercle passant :
- par chacun des milieux des trois côtés du triangle,
- par le pied de chacune des trois hauteurs du triangle,
- par le milieu de chacun des trois segments reliant l'orthocentre à un sommet du triangle.
De nombreux points remarquables du triangle sont situé sur ce cercle : de ce fait il possède plusieurs noms, parmi lesquels : cercle des neuf points, cercle de Feuerbach, Cercle de Terquem, cercle des 6, 12 ou 24 points, cercle médian, etc.
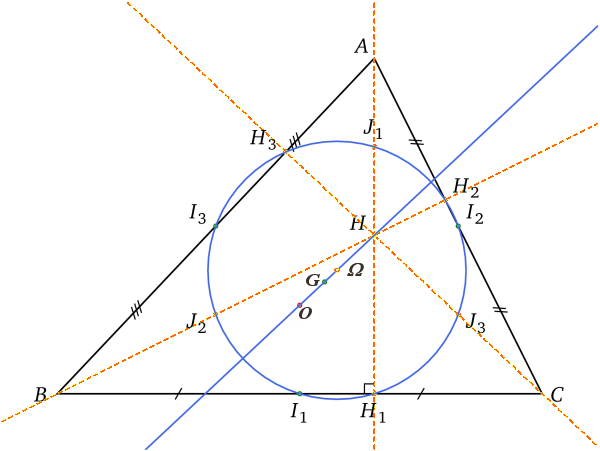
Définition et propriétés élémentaires
C'est le mathématicien Leonhard Euler qui a remarqué le premier que dans un triangle ABC le centre de gravité G, le centre du cercle circonscrit Ω et l'orthocentre H sont alignés. (Précisément, l'homothétie de centre G et de rapport
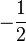
Notons I1 le milieu de [BC], I2 le milieu de [AC] et I3 le milieu de [AC]. Il n'est pas difficile de voir que cette même homothétie transforme le triangle ABC en le triangle I1I2I3 et le cercle circonscrit de ABC en cercle circonscrit à I1I2I3 : ce dernier cercle est précisément le cercle d'Euler.
Comme cette même homothétie transforme chaque hauteur de ABC en l'une de ses médiatrices, on a également que les pieds des hauteurs de ABC sont sur le cercle d'Euler et que chacun des milieux des segments [AH], [BH] et [CH] sont également sur le cercle d'Euler.
Découvertes
Brianchon, Poncelet et Feuerbach ont montré indépendamment et à des dates assez proches que les milieux des côtés et les pieds des hauteurs du triangle sont cocycliques, découvrant ainsi le cercle des 6 points.
Par la suite Olry Terquem ajoute à ce cercle les milieux des segments formés par les sommets du triangle et l'orthocentre : le cercle porte depuis le nom de cercle des 9 points.
En 1822, Karl Feuerbach démontre que le cercle des 9 points est tangent extérieurement aux cercles exinscrits et tangent intérieurement au cercle inscrit du triangle. Ce résultat s'appelle le théorème de Feuerbach (et les points de tangence sont les points de Feuerbach).
Depuis, on lui a ajouté quelques dizaines d'autres points remarquables du triangle
Quelques propriétés
- Le rayon du cercle d'Euler est la moitié du rayon du cercle circonscrit.
- Son centre est sur la droite d'Euler : on a : GH = 2ΩG (Voir relation d'Euler).
Hexagramme de Pascal
Une propriété projective que n'avait pas vue Euler:
- l'hexagramme H1I2H3I1H2I3H1 a pour droite de Pascal la droite d'Euler du triangle.