Droite d'Euler - Définition
En géométrie, la droite d'Euler d'un triangle est la droite passant par l'orthocentre, le centre du cercle circonscrit, le centre de gravité ou isobarycentre et le centre du cercle d'Euler de ce triangle.
Le centre du cercle d'Euler est situé au milieu du segment formé par l'orthocentre et le centre du cercle circonscrit. D'autre part, la distance entre le centre de gravité et l'orthocentre est le double de celle entre le centre de gravité et le centre du cercle circonscrit (voir : relation d'Euler).
C'est le mathématicien suisse Leonhard Euler qui démontra le premier que tous ces points étaient alignés. de plus, on sait grâce à cette propriété que :
ΩH = 3ΩG.
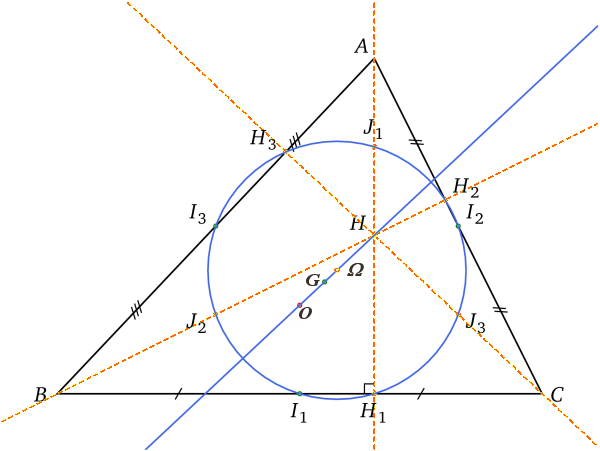
Cercle et droite d'Euler d'un triangle

















































