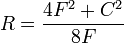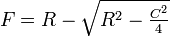Cercle - Définition

Introduction

Un cercle est une courbe plane fermée constituée des points situés à égale distance d'un point nommé centre. La valeur de cette distance est appelée rayon du cercle. Celui-ci étant infiniment variable, il existe donc une infinité de cercles pour un centre quelconque, dans chacun des plans de l'espace.

Dans le plan euclidien, il s'agit du « rond » qui est associé en français au terme de cercle. Dans un plan non euclidien ou dans le cas de la définition d'une distance non euclidienne, la forme peut être plus complexe. Dans un espace de dimensions quelconque, l'ensemble des points placés à une distance constante d'un centre est appelé sphère.

D'autres formes peuvent être qualifiées de « rondes » : les surfaces et solides dont certaines sections planes sont des cercles (cylindres, cônes, etc).

Pendant longtemps, le langage courant employait ce terme autant pour nommer la courbe (circonférence) que la surface qu'elle délimite. De nos jours, en mathématiques, le cercle désigne exclusivement la courbe ; la surface étant appelée disque.

Le rapport de la circonférence du cercle à son diamètre définit le nombre pi.

Géométrie euclidienne

Le cercle est une ellipse dont les foyers sont confondus au centre du cercle ; la longueur du grand axe est égale à la longueur du petit axe. C'est une conique dont l'excentricité e vaut 0. Elle peut être obtenue par l'intersection d'un plan avec un cône de révolution lorsque le plan est perpendiculaire à l'axe de révolution du cône (on parle parfois de « section droite » du cône).

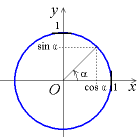
Dans un plan muni d'un repère orthonormé, le cercle unité ou cercle trigonométrique est le cercle dont le centre est l'origine du repère, et dont le rayon vaut 1.

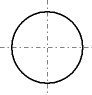
En dessin industriel, un cercle est le plus souvent représenté avec son axe horizontal et son axe vertical (en traits d'axe : trait fin composé de tirets longs et courts), ou bien simplement avec son centre matérialisé par une croix droite « + » en traits fins. Une forme de révolution, pleine ou creuse (cylindre, cône, sphère) et vue selon l'axe de révolution est représentée par un cercle.

Définitions

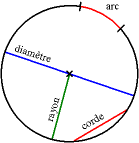
• Une corde est un segment de droite dont les extrémités se trouvent sur le cercle.
• Un arc est une portion de cercle délimitée par deux points.
• Une flèche est le segment reliant les milieux d'un arc de cercle et d'une corde définis par deux mêmes points.
• Un rayon est un segment de droite joignant le centre à un point du cercle.
• Un diamètre est une corde passant par le centre ; c'est un segment de droite qui délimite le disque en deux parts égales. Le diamètre est composé de deux rayons colinéaires ; sa longueur est 2r.
• Un disque est une région du plan limitée par un cercle.
• Un secteur circulaire est une partie du disque comprise entre deux rayons.
• Un angle au centre est un angle formé par deux rayons du cercle.

Propriétés géométriques

Voici quelques propriétés géométriques du cercle.

Mesures

La longueur d'un arc de rayon r sous-tendu par un angle α, exprimé en radians, est égale à αr. Ainsi, pour un angle de 2π (un tour complet), la longueur du cercle vaut 2πr.

La longueur d'une corde sous-tendue par un angle α est égale à 2rsin(α / 2).

L'aire du disque délimité par un cercle de rayon r vaut πr² ; si l'on prend une corde de longueur l donnée et que l'on s'en sert pour délimiter une surface fermée, la surface ayant la plus grande aire est délimitée par un cercle.

Selon la légende de la fondation de Carthage, le souverain avait permis aux Phéniciens de fonder une ville dont le pourtour serait délimité par une peau de vache ; Didon en fit une grande lanière et choisit une forme circulaire pour avoir la plus grande surface.

Tangente

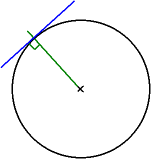
La tangente en un point du cercle est perpendiculaire au rayon en ce point.

Cette propriété a des applications en optique géométrique : un rayon lumineux passant par le centre d'un miroir sphérique repart en sens inverse selon la même direction (on a une réflexion perpendiculaire au miroir). Si l'on met une ampoule au centre d'un miroir sphérique, la lumière est renvoyée de l'autre côté, ce qui permet par exemple de « rabattre » la lumière vers un miroir parabolique (principe du contre-miroir).

Médiatrice

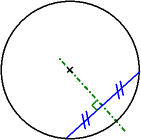
On peut montrer que la médiatrice d'une corde passe par le centre du cercle. Ceci permet de trouver le centre d'un cercle : il suffit de tracer deux cordes non parallèles et de rechercher l'intersection de leurs médiatrices.

On peut aussi montrer que les trois médiatrices d'un triangle sont concourantes et que le point de concours est le centre du cercle passant par les trois sommets, appelé cercle circonscrit au triangle.

Cercle et triangle rectangle

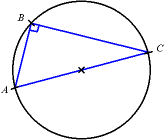
Prenons trois points du cercle A, B et C, dont deux — A et C — sont diamétralement opposés (c'est-à-dire sont les intersections du cercle avec un diamètre). Alors, ABC est un triangle rectangle en B.

Ceci découle du fait que la médiane de l'angle droit vaut la moitié de l'hypoténuse (on a un rayon et un diamètre) ; ceci est une propriété du triangle appelé dans les pays anglo-saxons le théorème de Thalès.

Angle inscrit, angle au centre

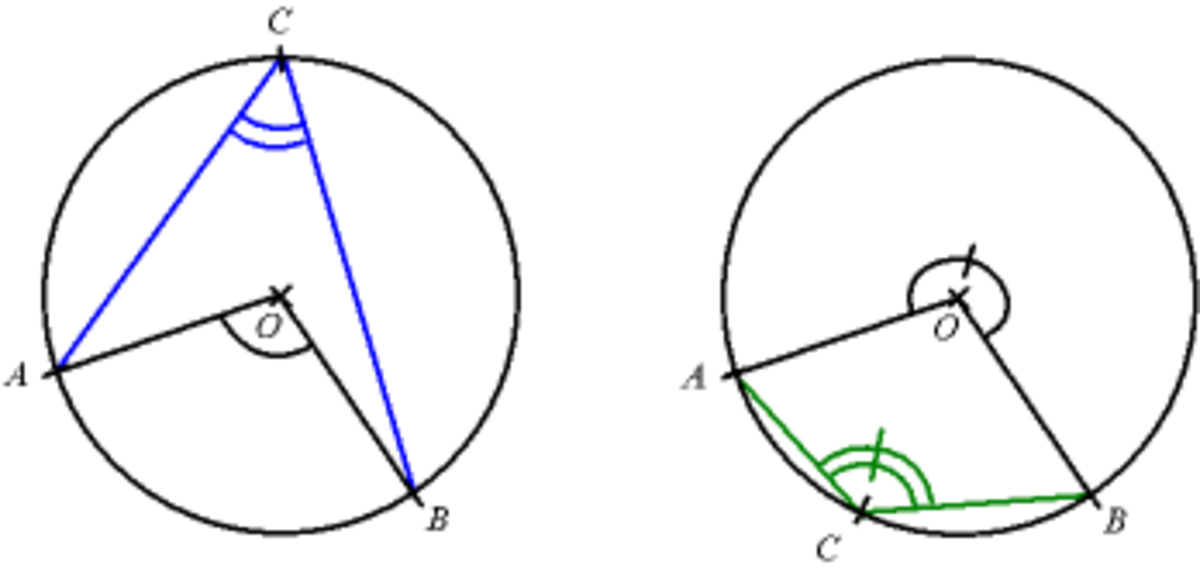
Prenons deux points distincts A et B du cercle. O est le centre du cercle et C est un autre point du cercle. Alors, on a

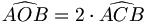
Pour l'angle au centre , il faut considérer le secteur angulaire qui intercepte l'arc opposé à l'arc contenant C.

Cette propriété est utilisée dans les appareils d'analyse spectrale par dispersion de longueur d'onde, c'est la notion de cercle de focalisation ou cercle de Rowland.

Points d'intersection avec une droite

Soit une droite (P₁P₂), ensemble des points P(x,y) tels que : P = P₁ + k(P₂ − P₁).

(x₁,y₁) et (x₂,y₂) étant les coordonnées des 2 points P₁ et P₂ de la droite et k un paramètre,

les coordonnées (x,y) d'un point P de la droite sont données par les deux équations paramétriques :

x = x₁ + k(x₂ − x₁),

y = y₁ + k(y₂ − y₁).

Un cercle de centre I(x₃,y₃) et de rayon r est défini par l'équation (x − x₃)² + (y − y₃)² = r². (C'est un simple calcul d'hypoténuse).

La substitution des coordonnées (x,y) d'un point de la droite dans l'équation du cercle donne une équation du deuxième degré d'inconnue k. Le discriminant de la forme b² − 4ac est donné par les coefficients :

a = (x₂ − x₁)² + (y₂ − y₁)²,

b = 2{(x₂ − x₁)(x₁ − x₃) + (y₂ − y₁)(y₁ − y₃)},

.

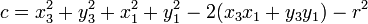
Trois cas pour b² − 4ac :

• Si b² − 4ac < 0 : pas d'intersection :
• Si b² − 4ac = 0 : la droite est tangente en un point au cercle. Dans ce cas
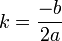
• Si b² − 4ac > 0 : il existe deux points d'intersection avec

et .

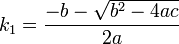
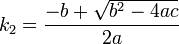
Rapport des cercles inscrits

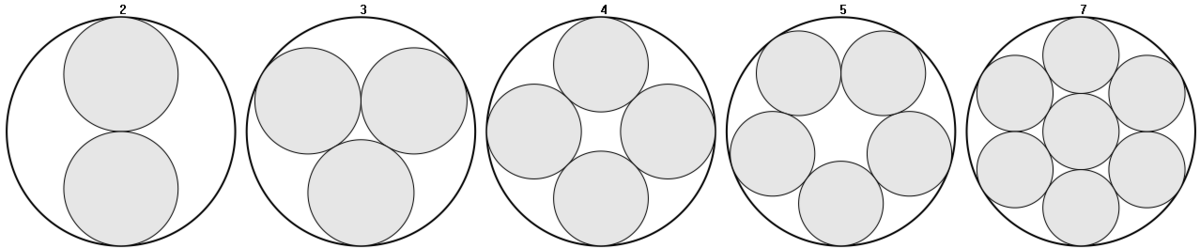
• Rayon R' des 2 plus grands cercles inscrits dans le cercle de rayon R et de surface S
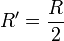
• Rayon R' et surface S' des 3 plus grands cercles inscrits
• Rayon R' et surface S' des 4 plus grands cercles inscrits
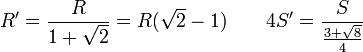
• Rayon R' des 5 plus grands cercles inscrits
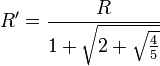
• Rayon R' des 7 plus grands cercles inscrits (1 cercle au centre entouré de 6)

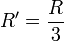
Puissance d'un point par rapport à un cercle

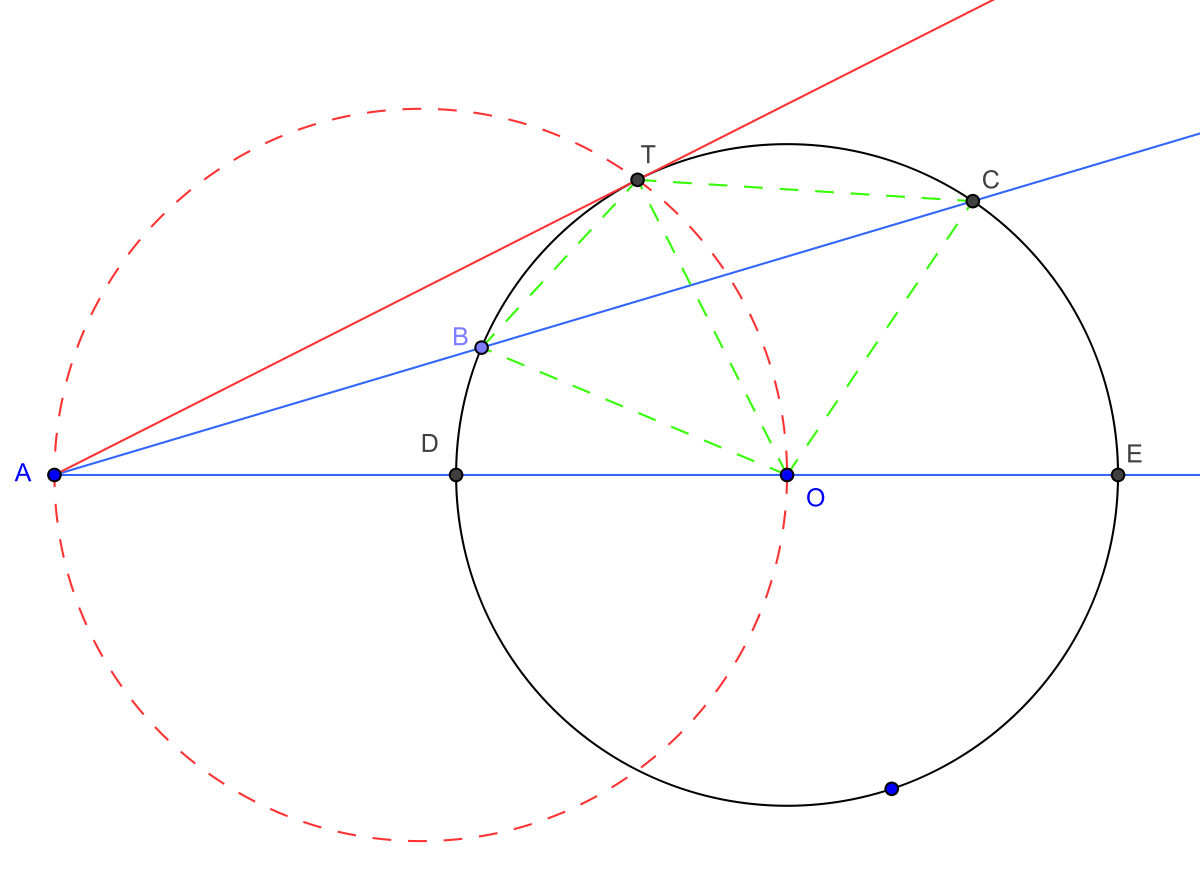
Si M est un point et Γ est un cercle de centre O et de rayon R, alors, pour toute droite passant par M et rencontrant le cercle en A et B, on a

.

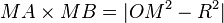
Cette valeur ne dépend pas de la droite choisie, mais seulement de la position de M par rapport au cercle.

On peut remarquer que

• si M est à l’extérieur du cercle,  ;
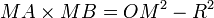
• si M est à l’intérieur du cercle,  ; ce produit correspond au produit des mesures algébriques MA et MB.

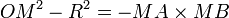
On appelle alors puissance du point M par rapport au cercle Γ le produit des mesures algébriques MA et MB. Ce produit est indépendant de la droite choisie et vaut toujours OM² − R².

Lorsque le point M est à l'extérieur du cercle, il est possible de mener des tangentes au cercle. En appelant T le point de contact d'une de ces tangentes, d'après le théorème de Pythagore dans le triangle OMT, la puissance de M est MT². L'égalité

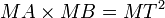
est suffisante pour affirmer que la droite (MT) est tangente au cercle.

La puissance d'un point permet de vérifier que quatre points sont cocycliques : en effet, si

• A, B, C, D sont quatre points tels que (AB) et (CD) se coupent en M et
• MA×MB = MC×MD (en mesures algébriques),

alors les quatre points sont cocycliques.

Équations

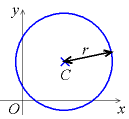
Dans un plan muni d'un repère orthonormé, l'équation du cercle de centre C(a,b) et de rayon r est :

(x − a)² + (y − b)² = r²

cette équation est en fait une application du théorème de Pythagore pour le triangle rectangle formé par le point du cercle et sa projection sur les deux rayons parallèles aux axes ; l'équation du cercle unité est donc

x² + y² = 1.

En mettant y en évidence, on obtient les équations cartésiennes du cercle :

.

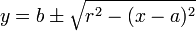
Les équations paramétriques du cercle sont

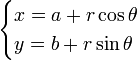
soit pour le cercle unité

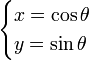
On peut également déterminer une équation pour le cercle de diamètre [AB] :

(x − x_A)(x − x_B) + (y − y_A)(y − y_B) = 0,

soit encore

x² + y² − (x_A + x_B)x − (y_A + y_B)y + x_Ax_B + y_Ay_B = 0.

On peut enfin exprimer le rayon, la corde et la flèche selon deux d'entre eux :