Hiérarchie arithmétique - Définition
En calculabilité, on considère les formules logiques (du premier ordre) de la forme
- formule

- formule

où φ ne contient pas de quantificateurs.
Ce genre de formules, dites prénexes, n'est pas un cas isolé, comme le prouve le théorème suivant :
Théorème : toute formule est équivalente à une formule Πn ou Σn, à moins qu'elle n'ait aucun quantificateur.
Preuve. On commence par placer tous les quantificateurs en tête de formule, grâce aux propriétés du type . Ensuite, pour obtenir l'alternance pour-tout/il-existe, on remplace une suite de k quantificateurs identiques par un quantificateur sur un k-uple:
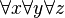
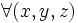
Par extension, on dira d'une formule qu'elle est Πn (respectivement Σn) si elle est équivalente à une formule Πn (respectivement Σn), même si elle n'est pas elle-même sous forme prénexe.
On dit qu'une formule est Δn si elle est à la fois Πn et Σn; Ainsi Δ0 désigne l'ensemble des formules sans quantificateurs.
On classifie ainsi toutes les formules comme Πn ou Σn, ce qui donne une manière de mesurer leur complexité, c'est-à-dire les moyens à employer pour les calculer. En particulier, les formules Σ1 expriment les ensembles récursivement énumérables.
Le théorème de Post fait plus précisément le lien entre hiérarchie arithmétique et degré de Turing.

















































