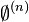Théorème de Post - Définition
Ce théorème fait le lien entre hiérarchie arithmétique et degré de Turing.
Théorème (Post): pour tout n>0
- B appartient à Σn + 1 si et seulement si B est récursivement énumérable avec oracle Πn (ou Σn).
-
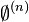
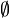
En particulier,
- B est dans Σn + 1 si et seulement si B est récursivement énumérable avec l'oracle
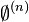
- B est dans Δn + 1 si et seulement si B est Turing-réductible à