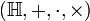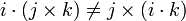Jeudi 12 Juin 2025
Rechercher 🔍

Algèbre sur un corps - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Définitions - Exemples d'algèbres de dimension finie - Bases et tables de multiplication d'une algèbre sur un corps - Contre-exemple

Bases et tables de multiplication d'une algèbre sur un corps

Tout espace vectoriel admet une base. Une base d'une algèbre A sur un corps K est une base de A pour sa structure d'espace vectoriel.

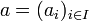
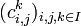
Si a=(a_i)_{i\in I} est une base de A, il existe alors une unique famille (c_{i,j}^k)_{i,j,k \in I} d'éléments du corps K tels que :

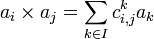
\displaystyle a_i\times a_j=\sum_{k\in I} c_{i,j}^k a_k .

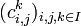
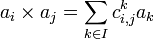
Pour i et j fixés, les coefficients sont nuls sauf un nombre fini d'entre eux. On dit que (c_{i,j}^k)_{i,j,k \in I} sont les constantes de structure de l'algèbre A par rapport à la base a, et que les relations a_i\times a_j=\sum_{k\in I} c_{i,j}^k a_k constituent la table de multiplication de l'algèbre A.

Contre-exemple

  • L'ensemble des quaternions (\mathbb H, +,\cdot, \times) n'est pas une \mathbb C -algèbre car la multiplication \times n'est pas \mathbb C -bilinéaire : i\cdot (j\times k)\neq j\times (i\cdot k) .
Exemples d'algèbres de dimension finie
- Introduction - Définitions - Exemples d'algèbres de dimension finie - Bases et tables de multiplication d'une algèbre sur un corps - Contre-exemple
miniature
🌱 La vie pourrait renaître sur Europe après la mort de la Terre
miniature
🌿 Confirmation scientifique: ce remède ancestral fait naturellement maigrir, et pas qu'un peu !
miniature
💥 Des astronomes identifient les plus puissantes explosions depuis le Big Bang
miniature
🦕 Ce crâne de stégosaure, le plus complet jamais découvert, réécrit l'histoire
miniature
🛏️ Les punaises de lit, ces compagnons indésirables depuis la préhistoire
miniature
🕸️ Connaissez-vous la toile cosmique, l'architecte de l'Univers ?
miniature
🌋 L'éruption de l'Etna vue depuis l'espace
miniature
🐋 Il y a 20 000 ans, l'Homme fabriquait des outils avec des os de baleines
miniature
🟠 Quel est le rôle de ce labyrinthe sur Mars ?
miniature
🎯 Cette stratégie innovante contre le cancer du sein offre une survie de 100%
miniature
1
💥 Le pulsar à trou noir: un objet qui intrigue les astrophysiciens
miniature
🐒 Première: ces singes kidnappent les bébés d'une autre espèce
miniature
🌍 Découverte d'une super-Terre à l'habitabilité intermittente
miniature
🧠 Ces cellules pourraient jouer un rôle bien plus important que les neurones dans la mémoire
miniature
🛰️ Une carte photographique de la Terre toutes les 35 minutes
miniature
Pourquoi l'oxygène est-il si indispensable à autant d'êtres vivants ?
miniature
🐱 Pourquoi certains chats miaulent et ronronnent plus que d'autres ?
miniature
Découverte: un antidouleur sans effets secondaires
miniature
1
🤔 Ces expériences remettent en question un concept fondamental de la thermodynamique
miniature
Le cannabis réduit de moitié la fonction des vaisseaux sanguins
miniature
Les différences hommes-femmes ne sont pas que génétiques
miniature
🦴 Des paresseux géants de plusieurs tonnes parcouraient autrefois l'Amérique
miniature
James Webb découvre une nouvelle population de trous noirs supermassifs
miniature
Le sol de l'Afrique du Sud s'est soulevé ces dernières années, pourquoi ?
miniature
👀 Ces lentilles de contact permettent de voir l'invisible
miniature
Révélations sur l'histoire de la lèpre en Amérique
miniature
Ce nouveau matériau possède des propriétés jamais vues !
miniature
😂 Que savons-nous réellement sur les chatouilles ?
miniature
1
Pour la lumière, le temps n'existe pas 🌟
miniature
Des scientifiques mesurent un ralentissement du vieillissement lié à ce cocktail
miniature
La tension de Hubble, mystère de l'expansion de l'Univers, enfin résolue ?
miniature
Voici comment les graisses saturées endommagent votre intestin en seulement deux jours
miniature
1
Les scientifiques réfléchissent à rendre Mars habitable
miniature
Cette empreinte digitale a 43 000 ans 🖐️
miniature
Un objet inconnu émet dans l'espace des signaux avec une régularité jamais vue 🛰
miniature
Comment la peste a évolué pour durer
miniature
Un indice de plus qu'Europe, lune de Jupiter, cacherait un océan salé sous sa glace
miniature
Le changement climatique menace l'accès à l'eau de 2 milliards de personnes
miniature
Le noyau de la Terre perd son or... qui remonte jusqu'en surface 🌍
miniature
Record d'efficacité pour des cellules solaires organiques
miniature
Cette galaxie bat tous les records de distance 🔭
miniature
Un monstre marin préhistorique enfin identifié après 35 ans de mystère
miniature
Pourquoi les constantes de l'Univers sont-elles si parfaites pour la vie ? 🤔
miniature
Découverte: cette combinaison de médicaments augmente la durée de vie de 30% 💊
miniature
Des fontaines de lave de la hauteur de la Tour Eiffel: éruptions à Hawaï 🌋
miniature
Quel est l'effet du café sur un cerveau endormi ?
miniature
La Lune, future plateforme économique de l'espace ? 🌕
miniature
Un test de la dépression chez les adolescents 🥺
miniature
D'où viennent ces dizaines de structures circulaires récentes sur Vénus ? ⭕
miniature
Pourquoi reconnaît-on visuellement un objet qu'on a seulement touché ? 👀
Page générée en 0.062 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise