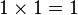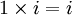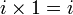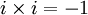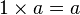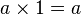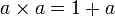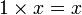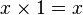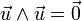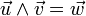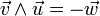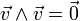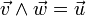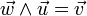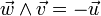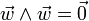Algèbre sur un corps - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une algèbre sur un corps commutatif est une structure algébrique qui se définit comme suit:
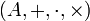


-

- (A, +, ·) est un espace vectoriel sur

- la loi × est définie de A x A dans A (loi de composition interne)
- la loi × est distributive par rapport à la loi + .
- pour tout (a, b) dans
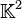
Définitions
Soient


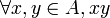
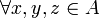
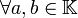
-
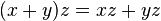
-
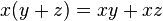
-
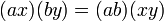
alors A est une algèbre sur



Deux algèbres A et B sur

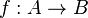
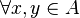
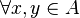
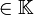
Dans la définition,




Exemples d'algèbres de dimension finie
- Algèbres associatives et commutatives
- L'ensemble des nombres complexes
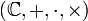

Une base de l'algèbre

|
|
|
|
|
|
- Tout corps fini est une algèbre associative, unifère et commutative de dimension n sur son sous-corps premier (
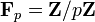
Par exemple le corps fini
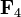
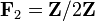
|
|
|
|
|
|
- On peut démontrer que toute algèbre unifère de dimension 2 sur un corps est associative et commutative. Sa table de multiplication dans une base (1, x) est de la forme :
|
|
|
|
| x2 = a1 + bx |
Une telle algèbre est appelée algèbre quadratique de type (a, b) (le type dépendant de la base choisie).
- Algèbres associatives et non commutatives
- L'ensemble des matrices carrées d'ordre
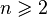

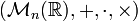

- L'ensemble des quaternions
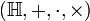

- L'ensemble des biquaternions
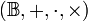

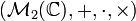

- Algèbre unifère non associative
- L'ensemble des octonions
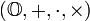

- Algèbres non associatives et non unifères
- L'espace euclidien
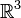
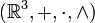

La table de multiplication dans une base orthonormale directe (


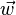
|
|
| , |
|
|
|
|
|
|
|
|
- L'ensemble des matrices carrées d'ordre
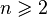

![\left(\mathcal M_n(\mathbb R), +,\cdot, [,] \right)](https://static.techno-science.net/illustration/Definitions/autres/4/49ebdc968ab715dec75900a90c652c57_fb48f0fc44240affab08920ff6c3069f.png)