Algorithme de Gauss-Newton - Définition

Algorithmes associés

Dans une méthode quasi-Newton, comme celle due à Davidon, Fletcher et Powell, une estimation de la matrice Hessienne, , est approchée numériquement en utilisant les premières dérivées .

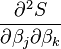
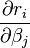
Une autre méthode pour résoudre les problèmes de moindres carrés en utilisant seulement les dérivées premières est la descente de gradient. Toutefois, cette méthode ne prend pas en compte les dérivées secondes, même sommairement. Par conséquent, cette méthode s'avère particulièrement inefficace pour beaucoup de fonctions.

Versions améliorées

Avec la méthode de Gauss–Newton, la somme des carrés S peut ne pas décroître à chaque itération. Toutefois, puisque est une direction de descente, à moins que soit un point stationnaire, il se trouve que pour tout α > 0 suffisamment petit. Ainsi, en cas de divergence, une solution est d'employer une fraction, α, de l'incrément, dans la formule de mise à jour

.

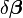
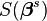
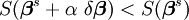
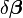
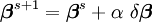
En d'autres termes, le vecteur d'incrément est trop long, mais pointe bien vers le bas, si bien que parcourir une fraction du chemin fait décroître la fonction objectif S. Une valeur optimale pour α peut être trouvée en utilisant un algorithme de Recherche linéaire: la magnitude de α est déterminée en trouvant le minimum de S en faisant varier α sur une grille de l'intervalle 0 < α < 1.

Dans le cas où la direction de l'incrément est telle que α est proche de zéro, une méthode alternative pour éviter la divergence est l'algorithme de Levenberg-Marquardt. Les équations normales sont modifiées de telle sorte que l'incrément est décalé en direction de la descente la plus forte

,

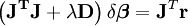
où D est une matrice diagonale positive. Remarquons que lorsque D est la matrice identité et que , alors , par conséquent la direction de s'approche de la direction du gradient .

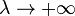
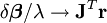
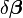
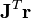
Le paramètre de Marquardt, λ, peut aussi être optimisé par une méthode de recherche linéaire, mais ceci rend la méthode fort inefficace dans la mesure où le vecteur d'incrément doit être re-calculé à chaque fois que λ change.