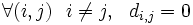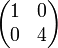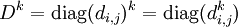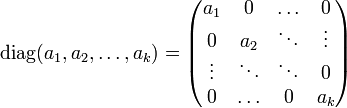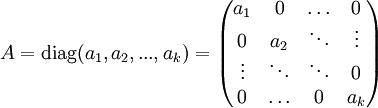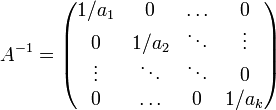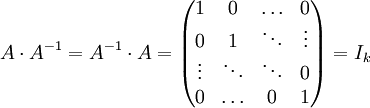Matrice diagonale - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En algèbre linéaire, une matrice diagonale est une matrice carrée dont les coefficients en dehors de la diagonale principale sont nuls. Les coefficients de la diagonale peuvent être ou ne pas être nuls. Ainsi, la matrice D = (di,j) est diagonale si :
Exemple :
On remarque qu'une matrice diagonale est une matrice qui correspond à la représentation d'un endomorphisme diagonalisable dans une base de vecteurs propres. La matrice d'un endomorphisme diagonalisable est semblable à une matrice diagonale.
Toute matrice diagonale est aussi une matrice symétrique, une matrice normale et une matrice triangulaire. La matrice identité In est diagonale.
Utilisations
Les matrices diagonales apparaissent dans presque tous les domaines de l'algèbre linéaire. La multiplication de matrices diagonales est très simple ; aussi, si une matrice intéressante peut d'une certaine façon être remplacée par une matrice diagonale, alors les calculs qui l'impliquent seront plus rapides et la matrice plus facile à stocker en mémoire. Un procédé permettant de rendre certaines matrices diagonales est la diagonalisation.
Une matrice presque diagonale (on la dit alors matrice à diagonale dominante) peut être inversée sous réserve de non-intersection de ses cercles de Gershgorin.
Une matrice diagonale d'ordre n possède de manière naturelle des colonnes propres qui sont les matrices des coordonnées de n vecteurs orthonormés et ses coefficients diagonaux sont exactement les valeurs propres associées.
Voir aussi la décomposition en valeurs singulières, d'après laquelle toute matrice est unitairement équivalente à une matrice diagonale positive.
Multiplication
Les matrices diagonales forment une sous-algèbre commutative de
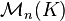
En d'autres termes, si les matrices D = diag(di) et E = diag(ei) sont diagonales, alors :
- λD + μE = F est une matrice diagonale
- DE = ED = G est une matrice diagonale
avec
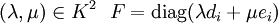
Ainsi les matrices diagonales peuvent simplement être multipliées coefficients par coefficients, parce que les zéros en dehors de la diagonale annulent les autres termes dans la formule de multiplication.
Une conséquence de cela est qu'élever une matrice diagonale A à une certaine puissance revient à élever les coefficients de la diagonale de A à cette puissance :
Notation
Comme seuls les éléments de la diagonale peuvent être non nuls, une notation courante des matrices diagonales est la suivante.
Inversion
Une matrice diagonale d'éléments diagonaux tous non nuls est toujours inversible, et l'opération est immédiate. En effet, si
alors
On vérifie bien que
soit la matrice identité.