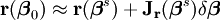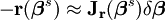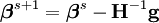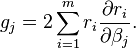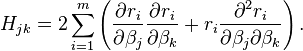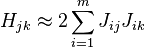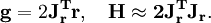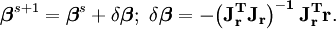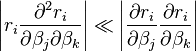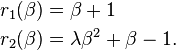Algorithme de Gauss-Newton - Définition

Remarques

L'hypothèse m≥n est nécessaire, car dans le cas contraire la matrice serait non inversible et les équations normales ne pourraient être résolues.

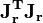
L'algorithme de Gauss–Newton peut être dérivé par approximation linéaire du vecteur de fonctions r_i. En utilisant le Théorème de Taylor, on peut écrire qu'à chaque itération

avec ; notons que représente la vraie valeur des paramètres pour laquelle les résidus s'annulent. Trouver l'incrément revient à résoudre

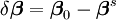
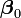
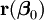
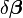
ce qui peut se faire par la technique classique de régression linéaire et qui fournit exactement les équations normales.

Les équations normales sont un système de m équations linéaires d'inconnu . Ce système peut se résoudre en une étape, en utilisant la factorisation de Cholesky ou, encore mieux, la décomposition QR de J_r. Pour de grands systèmes, une méthode itérative telle que la méthode du gradient conjugué peut être plus efficace. S'il existe une dépendance linéaire entre les colonnes J_r, la méthode échouera car deviendra singulier.

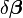
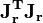
Dérivation à partir de la méthode de Newton

Dans ce qui suit, l'algorithme de Gauss–Newton sera tiré de l'algorithme d'optimisation de Newton; par conséquent, la vitesse de convergence sera au plus quadratique.

La relation de récurrence de la méthode de Newton pour minimiser une fonction S de paramètres , est

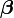
où g représente le gradient de S et H sa matrice hessienne. Puisque , le gradient est

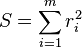
Les éléments de la Hessienne sont calculés en dérivant les éléments du gradient, g_j, par rapport à β_k

La méthode de Gauss–Newton est obtenue en ignorant les dérivées d'ordre supérieur à deux. La Hessienne est approchée par

où est l'élément (i,j) de la jacobienne . Le gradient et la hessienne approchée sont alors

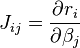
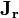
Ces expressions sont replacées dans la relation de récurrence initiale afin d'obtenir la relation récursive

La convergence de la méthode n'est pas toujours garantie. L'approximation

doit être vraie pour pouvoir ignorer les dérivées du second ordre. Cette approximation peut être valide dans deux cas, pour lesquels on peut s'attendre à obtenir la convergence:

1. Les valeurs de la fonction r_i sont petites en magnitude, au moins près du minimum;
2. Les fonctions sont seulement faiblement non-linéaires, si bien que est relativement petit en magnitude.

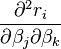
Propriété de convergence

On peut démontrer que l'incrément δβ est une direction de descente pour S, et que si l'algorithme converge, alors la limite est un point stationnaire pour la somme des carrés S. Toutefois, la convergence n'est pas garantie, pas plus qu'une convergence locale contrairement à la méthode de Newton.

La vitesse de convergence de l'algorithme de Gauss–Newton peut approcher la vitesse quadratique. L'algorithme peut converger lentement voire ne pas converger du tout si le point de départ de l'algorithme est trop loin du minimum ou si la matrice est mal conditionnée.

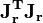
L'algorithme peut donc échouer à converger. Par exemple, le problème avec m = 2 équations et n = 1 variable, donné par

L'optimum se situe en β = 0. Si λ = 0 alors le problème est en fait linéaire et la méthode trouve la solution en une seule itération. Si |λ| < 1, alors la méthode converge linéairement et les erreurs décroissent avec un facteur |λ| à chaque itération. Cependant, si |λ| > 1, alors la méthode ne converge même pas localement.