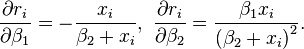Algorithme de Gauss-Newton - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'algorithme de Gauss-Newton est une méthode de résolution des problèmes de moindres carrés non-linéaires. Elle peut être vue comme une modification de la méthode de Newton dans le cas multidimensionnel afin de trouver le minimum d'une fonction (à plusieurs variables). Mais l'algorithme de Gauss-Newton est totalement spécifique à la minimisation d'une somme de fonctions au carré et présente le grand avantage de ne pas nécessiter les dérivées secondes, parfois complexes à calculer.
Les problèmes de moindres carrés non-linéaires surviennent par exemple dans les problèmes de régressions non-linéaires, où des paramètres du modèle sont recherchés afin de correspondre au mieux aux observations disponibles.
Cette méthode est due au mathématicien renommé Carl Friedrich Gauss.
Algorithme
Soit m fonctions ri (
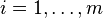
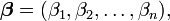
En débutant avec l'approximation initiale
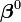
où l'incrément
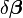
Ici, on note par r le vecteur des fonctions ri, et par Jr la matrice jacobienne m×n de r par rapport à β, tous les deux évalués en βs. La matrice transposée est notée à l'aide de l'exposant T.
Dans les problèmes d'ajustement des données, où le but est de trouver les paramètres
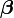
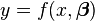
Alors, l'incrément
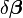
Dans tous les cas, une fois connu l'estimation à l'étape s, les équations normales permettent de trouver l'estimation à l'étape suivante; pour résumer, on a:
L'ensemble du terme de droite est calculable car ne dépend que de
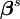
Exemple
Dans cet exemple, l'algorithme de Gauss–Newton est utilisé pour ajuster un modèle en minimisant la somme des carrés entre les observations et les prévisions du modèle.
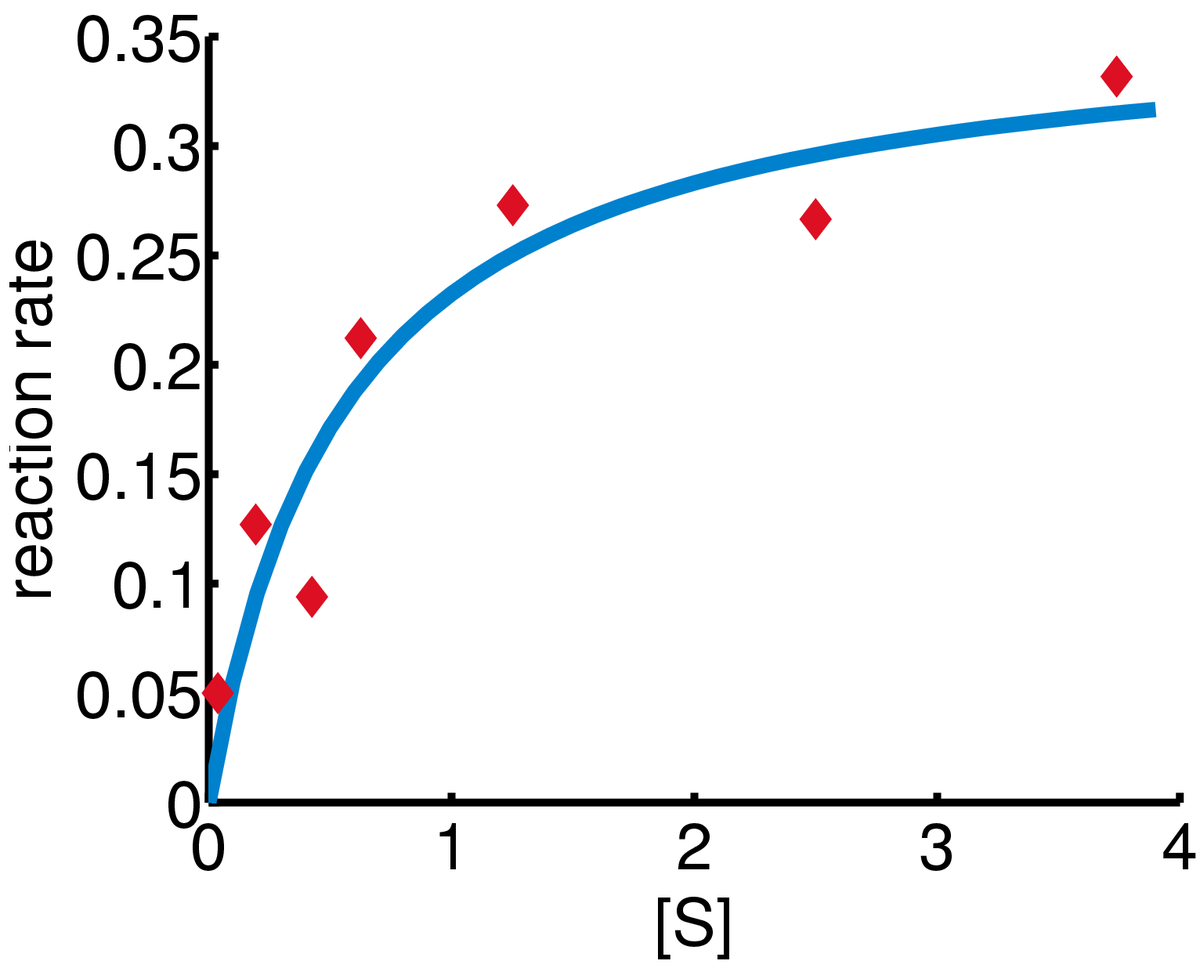
Dans une expérience de biologie, on étudie la relation entre la concentration du substrat [S] et la vitesse de réaction dans une réaction enzymatique à partir de données reportées dans le tableau suivant.
-
i 1 2 3 4 5 6 7 [S] 0.038 0.194 0.425 0.626 1.253 2.500 3.740 rate 0.050 0.127 0.094 0.2122 0.2729 0.2665 0.3317
On souhaite ajuster les données à la courbe de la forme:
L'estimation par moindres carrés porte sur les paramètres Vmax et KM.
On note xi et yi les valeurs de [S] et la vitesse de réaction, pour
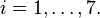
-
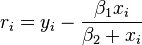
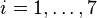
La jacobienne
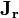
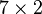
Commençant avec l'estimation initiale β1=0,9 et β2=0,2, il suffit de 5 itérations de l'algorithme de Gauss–Newton pour atteindre les estimations optimales
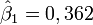
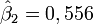
-
Itération Estimation Somme des carrés des résidus 1 [0,9;0,2] 1,4455000 2 [0,33266;0,26017] 0,0150721 3 [0,34281;0,42608] 0,0084583 4 [0,35778;0,52951] 0,0078643 5 [0,36141;0,55366] 0,0078442 6 [ 0,3618;0,55607] 0,0078440
La figure ci-contre permet de juger de l'adéquation du modèle aux données en comparant la courbe ajustée (bleue) aux observations (rouge).
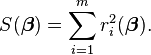
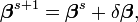
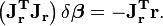
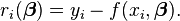
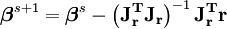
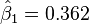
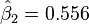
![\text{rate}=\frac{V_{max}[S]}{K_M+[S]}](https://static.techno-science.net/illustration/Definitions/autres/1/1443af08bc7bac08c61cd68233f4f8e1_c825927b460793423479546db47ec666.png)