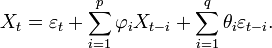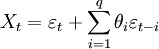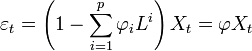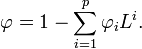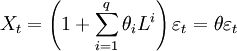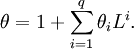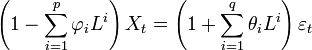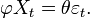Arma - Définition

Modèle autorégressif et moyenne-mobile

La notation ARMA(p, q) réfère le modèle avec p termes autoregressifs et q termes moyenne-mobile. Ce modèle contient à la fois les modèles AR(p) et MA(q) :

Modèle moyenne mobile

La notation MA(q) réfère au modèle moyenne-mobile d'ordre q :

où les θ₁, ..., θ_q sont les paramètres du modèle et ε_t, ε_t-1,... sont encore une fois des termes d'erreur.

Spécification en termes de l'opérateur de retard

Les modèles ARMA peuvent s'écrire en termes de L, qui est l'opérateur retard. Le modèle autorégressif AR(p) s'écrit

où φ représente le polynôme

Pour le modèle moyenne mobile MA(q), on a

où θ représente le polynôme

Finalement, en combinant les deux aspects, on en tire l'écriture du modèle ARMA(p, q) :

où plus court :

Une note sur les termes d'erreur

Les termes d'erreur ε_t sont généralement supposés indépendants et identiquement distribués (i.i.d.) selon une loi normale de moyenne nulle : ε_t ~ N(0,σ²) où σ² est la variance. Ces hypothèses peuvent être assouplies mais ceci changerait les propriétés du modèle, comme par exemple supposer le simple caractère i.i.d.

Modèle d'ajustement

Les modèles ARMA, une fois choisi les ordres p et q, peuvent être ajustés sur des données par la méthode des moindres carrés : on recherche les paramètres qui minimisent la somme des carrés des résidus. Prendre des valeurs de p et q les plus petites est généralement vu comme une bonne pratique (principe de parcimonie). Pour un modèle AR pur, les équations de Yule-Walker permettent de réaliser l'ajustement.