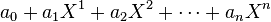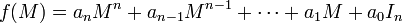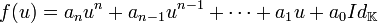Polynôme - Définition

Introduction

Courbe polynomiale cubique

Un polynôme, en mathématiques, est la combinaison linéaire des produits de puissances d'une ou de plusieurs indéterminées, habituellement notées X, Y, Z… Ces objets sont largement utilisés en pratique, ne serait-ce que parce qu'ils donnent localement une valeur approchée de toute fonction dérivable (voir développement limité) et permettent de représenter des formes lisses (voir l'article courbe de Bézier, décrivant un cas particulier de fonction polynôme).

Un polynôme, en algèbre générale, à une indéterminée sur un anneau unitaire est une expression de la forme :

où X est un symbole appelé indéterminée du polynôme, supposé être distinct de tout élément de l'anneau, et les coefficients a_i sont dans l'anneau.

Si, en mathématiques appliquées, en analyse et en algèbre linéaire, il est fréquent de confondre le polynôme avec la fonction polynôme, il n'en est pas de même en algèbre générale. Cet article traite principalement du polynôme formel à une indéterminée.

Considérations historiques

L'histoire des polynômes est inséparable de celle de l'algèbre. Initialement créés pour résoudre des équations, ils se trouvent confondus avec les fonctions polynômes. Au fur et à mesure que les recherches s'approfondissent, il se révèle nécessaire de distinguer plus nettement le polynôme formel de la fonction polynôme. Cette évolution se fait conjointement avec le développement de l'algèbre générale. Les coefficients quittent alors le domaine des nombres usuels, comme les réels ou les complexes pour appartenir à des anneaux commutatifs unitaires ou des corps quelconques. L'étude des polynômes formels ouvre la porte à celle des séries formelles.

Fonctions polynômes

À tout polynôme f(X) de A[X], on peut associer une fonction polynôme f d'ensemble de définition et d'arrivée A. On obtient la valeur de cette fonction pour un argument donné a en remplaçant partout le symbole X dans f(X) par a. Les algébristes font une distinction entre un polynôme et une fonction polynomiale car, sur certains anneaux A (par exemple sur les corps finis), deux polynômes différents peuvent avoir la même fonction polynôme associée. Ceci n'est pas le cas sur le corps des réels ou des complexes et donc les « analystes » ne séparent pas les deux concepts.

Exemple : Sur le corps fini , le polynôme X + X² est non nul, mais sa fonction polynôme associée l'est.

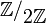
Morphisme d'évaluation : Plus généralement, dans un polynôme f(X), on peut remplacer le symbole X par n'importe quel élément appartenant à une algèbre E sur A. L'application qui, à tout polynôme f(X) dans A[X], associe l'élément de E (défini comme ci-dessus), est appelée morphisme d'évaluation en de A[X] dans E et noté f. Un cas très fréquent est celui où A est un corps , et E l'algèbre des matrices n × n sur , ou bien l'algèbre des endomorphismes d'un espace vectoriel sur . On définit ainsi des polynômes de matrices et d'endomorphismes :

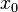
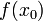
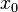
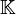
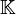
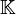
On remarque que les deux polynômes ci-dessus sont différents mais que le morphisme d'évaluation qui leur est associée est identique. Ainsi f est un morphisme d'évaluation alors que f(u) est un polynôme d'endomorphismes, f(M) est un polynôme de matrices, et f(X) est un polynôme d'indéterminée X, plus sobrement appelé polynôme.

Une fonction polynômiale est la restriction de l'endomorphisme d'évaluation aux éléments du corps de base, ici A.