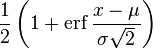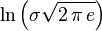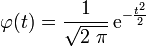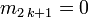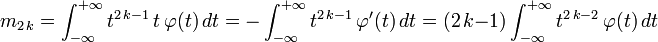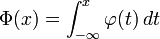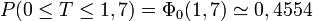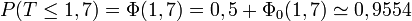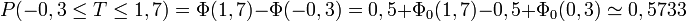Loi normale - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Distribution gaussienne | |
|---|---|
| |
| |
| | |
| Paramètres | μ moyenne (nombre réel) σ2 > 0 variance (nombre réel) |
| Support |
|
| Densité de probabilité (fonction de masse) |
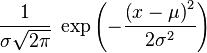
|
| Fonction de répartition |
|
| Espérance | μ |
| Médiane (centre) | μ |
| Mode | μ |
| Variance | σ2 |
| Asymétrie (statistique) | 0 |
| Kurtosis (non-normalisé) | 3 (0 si normalisé) |
| Entropie |
|
| Fonction génératrice des moments |
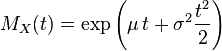
|
| Fonction caractéristique |
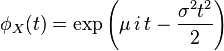
|
| modifier | |
En probabilité, on dit qu'une variable aléatoire réelle X suit une loi normale (ou loi normale gaussienne, loi de Laplace-Gauss) d'espérance μ et d'écart type σ strictement positif (donc de variance σ2) si cette variable aléatoire réelle X admet pour densité de probabilité la fonction p(x) définie, pour tout nombre réel x, par :
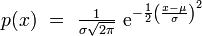
Une telle variable aléatoire est alors dite variable gaussienne.
On note habituellement cela de la manière suivante :
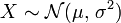
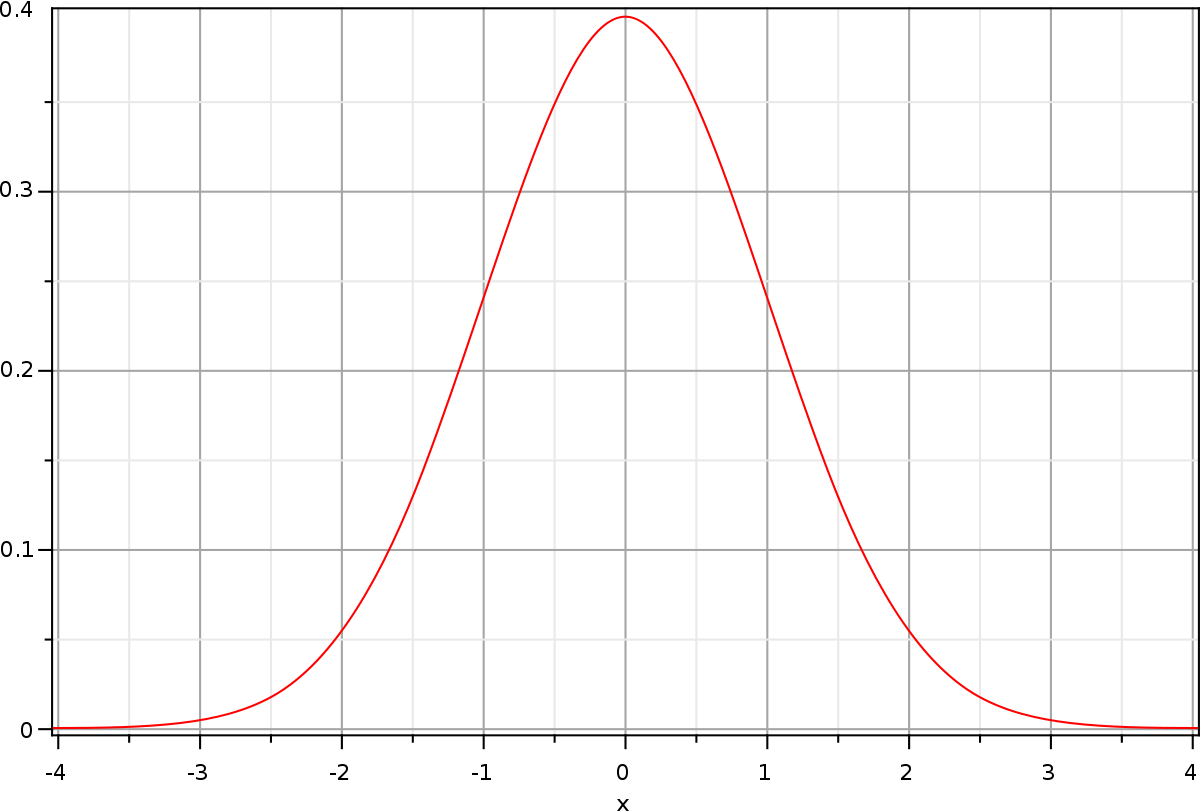
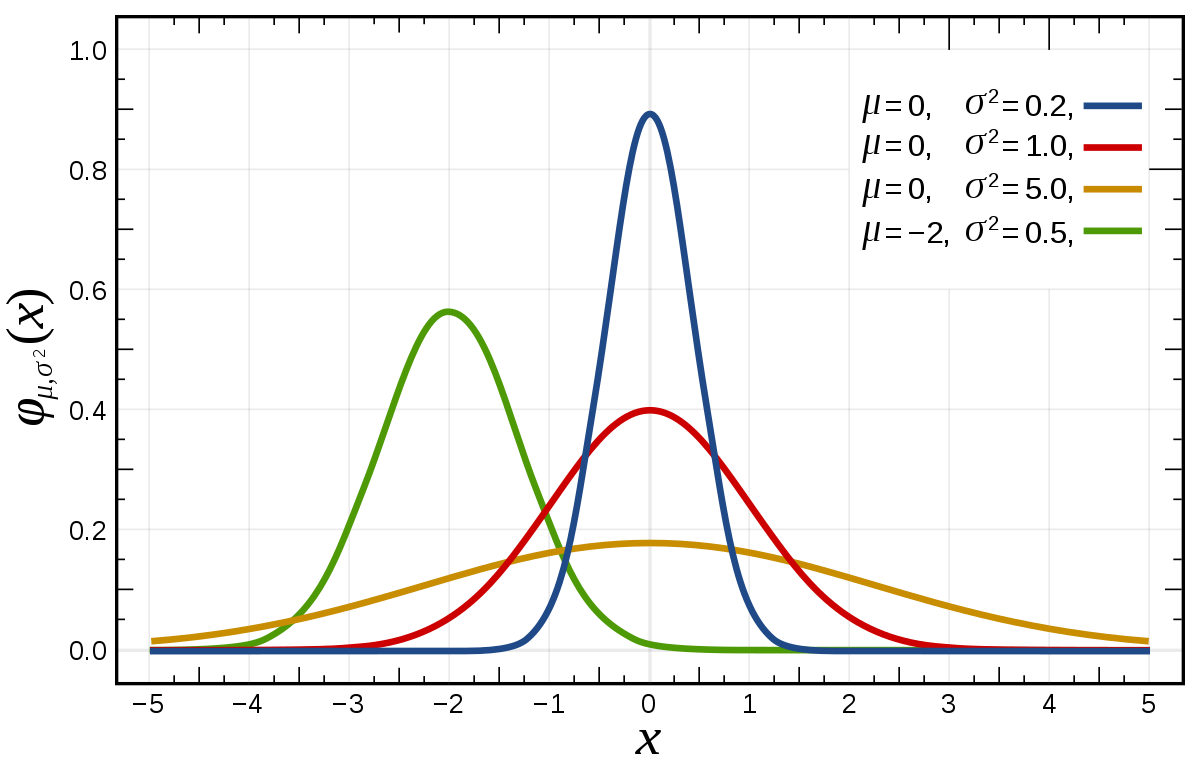
La loi normale est une des principales distributions de probabilité. Elle a été introduite par le mathématicien Abraham de Moivre en 1733 et utilisée par lui afin d'approcher des probabilités associées à des variables aléatoires binomiales possédant un paramètre n très grand. Cette loi a été mise en évidence par Gauss au XIXe siècle et permet de modéliser de nombreuses études biométriques. Sa densité de probabilité dessine une courbe dite courbe en cloche ou courbe de Gauss.
La loi normale centrée réduite
Définition
On appelle loi normale (ou gaussienne) centrée réduite la loi définie par la densité de probabilité
On vérifie qu'elle est continue et que son intégrale sur
On sait en effet que
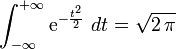
On démontre (voir plus bas) que la loi définie par cette densité de probabilité admet une espérance nulle et une variance égale à 1.
Remarques :
- la densité
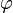
- elle est indéfiniment dérivable et vérifie, pour tout
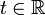
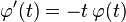
La représentation graphique de cette densité est une courbe en cloche (ou courbe de Gauss).
Moments
Les moments de cette loi existent tous. Pour tout
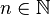
-
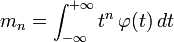
Pour la suite on supposera μ = 0 et σ2 = 1.
- En raison de la parité de l'intégrande, tous les moments d'ordre impair sont nuls :
- Supposons à présent n pair :
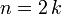
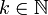
- Si
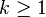
- ce qui fournit la relation de récurrence :
-
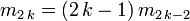
- De cette relation, on déduit, comme
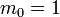
-
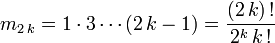
- En particulier,
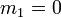
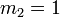
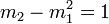
- Ceci justifie l'appellation de loi normale centrée réduite.
- Des formules précédentes, on déduit encore :
-
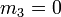
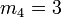
- La loi étant réduite, les moments centrés sont tous égaux aux moments par rapport à l'origine de même rang ; en particulier :
-
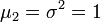
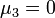
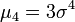
- On en déduit l'asymétrie (skewness) :
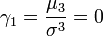
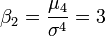
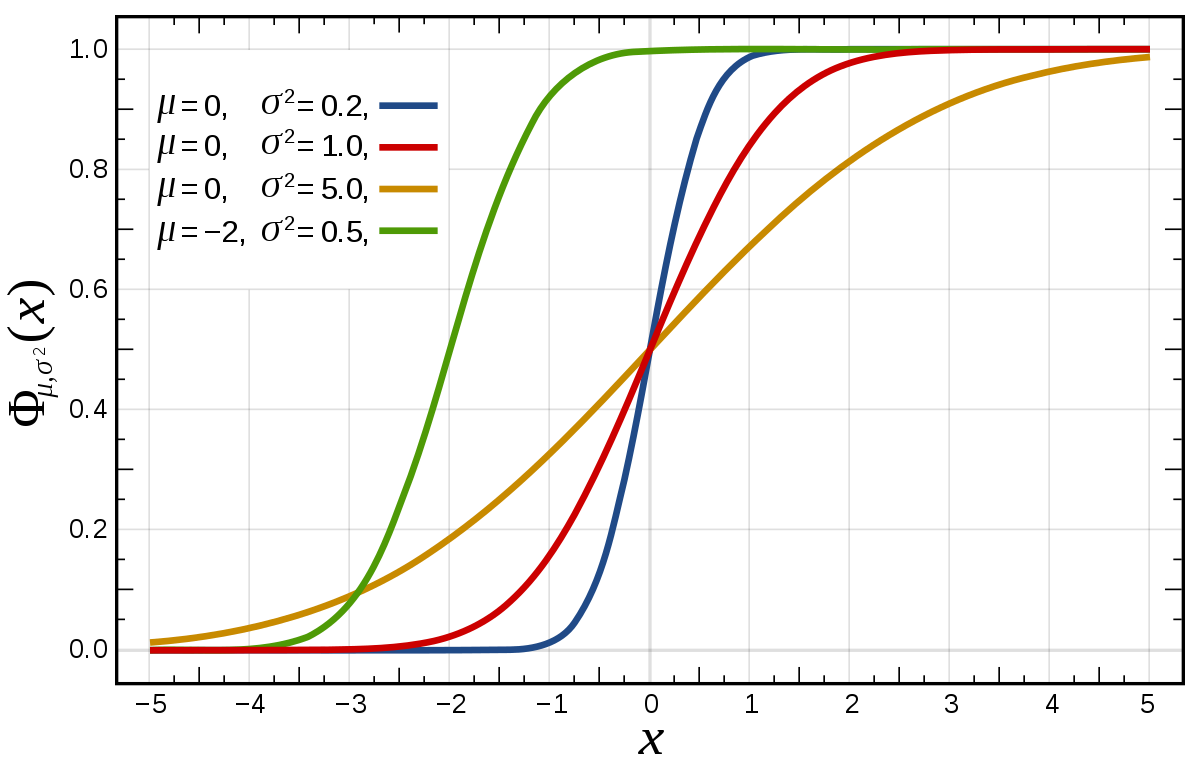
Fonction de répartition
On note Φ la fonction de répartition de la loi normale centrée réduite. Elle est définie, pour tout réel x, par :
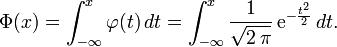
Φ est la primitive de

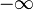
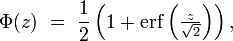
ou bien encore
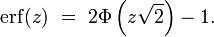
Citons les propriétés suivantes de la fonction Φ :
- Elle est indéfiniment dérivable, et
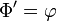
- Elle est strictement croissante, tend vers 0 en
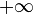
- (c'est donc une bijection
![\R \to\, ]0,\, 1[\,](https://static.techno-science.net/illustration/Definitions/autres/5/57e1b51edc83a9645ee6f7baea82c185_cfde1c57392168dc6c2c281fb18e1fdd.png)
![p \in\, ]0,\, 1[\,](https://static.techno-science.net/illustration/Definitions/autres/f/ffcce36c227a3b4d9dac45ad5299069e_225a9c89c3fa45fda48b756e51a99cf4.png)
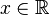
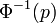
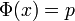
- Pour tout
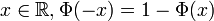
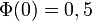
Remarque : les notations

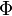
Approximation de la fonction de répartition
Il n'existe pas d'expression pour Φ mais on peut exploiter avec profit son aspect régulier pour en donner une approximation grâce à un développement en série de Taylor. Par exemple, voici une approximation (à l'ordre 5) autour de 0:
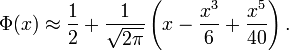
Cette approximation est performante pour | x | < 2.
Une approximation pour les grandes valeurs de x est donnée, pour x positif, par la formule
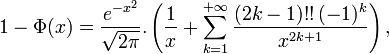
série divergente pour tout x positif, mais dont les sommes partielles encadrent 1-Φ(x) de manière efficace lorsque x est grand. Par exemple,
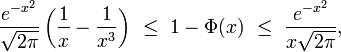
d'où une erreur relative inférieure à 25% pour x supérieur à 2 ou bien inférieure à 11% pour x supérieur à 3. Ou bien encore :
d'où une erreur relative inférieure à 25% pour x supérieur à 2 ou bien inférieure à 2% pour x supérieur à 3.
Tables numériques
Il existe des tables de la fonction de répartition, donnant des valeurs approchées de
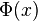

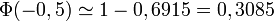
Au lieu des précédentes, on utilise souvent des tables de la fonction qu'on notera ici
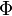
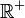
La table suivante donne pour tout x de 0 jusqu'à 3,9 par pas de 0,01, la valeur de 105 Φ(x). Ces valeurs sont arrondies à l'unité la plus proche.
L'entrée en ligne donne les deux premiers chiffres de x, c'est-à-dire le chiffre des unités et celui des dixièmes, et l'entrée en colonne le chiffre des centièmes.
Par exemple : Pour Φ(1,73) = 0,95818, on choisira 1,7 en ligne et 0,03 en colonne (1,7 + 0,03 = 1.73) et l'intersection nous donnera le résultat.
| 0,00 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0,0 | 50000 | 50399 | 50798 | 51197 | 51595 | 51994 | 52392 | 52790 | 53188 | 53586 |
| 0,1 | 53983 | 54380 | 54776 | 55172 | 55567 | 55962 | 56356 | 56749 | 57142 | 57535 |
| 0,2 | 57926 | 58317 | 58706 | 59095 | 59483 | 59871 | 60257 | 60642 | 61026 | 61409 |
| 0,3 | 61791 | 62172 | 62552 | 62930 | 63307 | 63683 | 64058 | 64431 | 64803 | 65173 |
| 0,4 | 65542 | 65910 | 66276 | 66640 | 67003 | 67364 | 67724 | 68082 | 68439 | 68793 |
| 0,5 | 69146 | 69497 | 69847 | 70194 | 70540 | 70884 | 71226 | 71566 | 71904 | 72240 |
| 0,6 | 72575 | 72907 | 73237 | 73565 | 73891 | 74215 | 74537 | 74857 | 75175 | 75490 |
| 0,7 | 75804 | 76115 | 76424 | 76730 | 77035 | 77337 | 77637 | 77935 | 78230 | 78524 |
| 0,8 | 78814 | 79103 | 79389 | 79673 | 79955 | 80234 | 80511 | 80785 | 81057 | 81327 |
| 0,9 | 81594 | 81859 | 82121 | 82381 | 82639 | 82894 | 83147 | 83398 | 83646 | 83891 |
| 1,0 | 84134 | 84375 | 84614 | 84849 | 85083 | 85314 | 85543 | 85769 | 85993 | 86214 |
| 1,1 | 86433 | 86650 | 86864 | 87076 | 87286 | 87493 | 87698 | 87900 | 88100 | 88298 |
| 1,2 | 88493 | 88686 | 88877 | 89065 | 89251 | 89435 | 89617 | 89796 | 89973 | 90147 |
| 1,3 | 90320 | 90490 | 90658 | 90824 | 90988 | 91149 | 91309 | 91466 | 91621 | 91774 |
| 1,4 | 91924 | 92073 | 92220 | 92364 | 92507 | 92647 | 92785 | 92922 | 93056 | 93189 |
| 1,5 | 93319 | 93448 | 93574 | 93699 | 93822 | 93943 | 94062 | 94179 | 94295 | 94408 |
| 1,6 | 94520 | 94630 | 94738 | 94845 | 94950 | 95053 | 95154 | 95254 | 95352 | 95449 |
| 1,7 | 95543 | 95637 | 95728 | 95818 | 95907 | 95994 | 96080 | 96164 | 96246 | 96327 |
| 1,8 | 96407 | 96485 | 96562 | 96638 | 96712 | 96784 | 96856 | 96926 | 96995 | 97062 |
| 1,9 | 97128 | 97193 | 97257 | 97320 | 97381 | 97441 | 97500 | 97558 | 97615 | 97670 |
| 2,0 | 97725 | 97778 | 97831 | 97882 | 97932 | 97982 | 98030 | 98077 | 98124 | 98169 |
| 2,1 | 98214 | 98257 | 98300 | 98341 | 98382 | 98422 | 98461 | 98500 | 98537 | 98574 |
| 2,2 | 98610 | 98645 | 98679 | 98713 | 98745 | 98778 | 98809 | 98840 | 98870 | 98899 |
| 2,3 | 98928 | 98956 | 98983 | 99010 | 99036 | 99061 | 99086 | 99111 | 99134 | 99158 |
| 2,4 | 99180 | 99202 | 99224 | 99245 | 99266 | 99286 | 99305 | 99324 | 99343 | 99361 |
| 2,5 | 99379 | 99396 | 99413 | 99430 | 99446 | 99461 | 99477 | 99492 | 99506 | 99520 |
| 2,6 | 99534 | 99547 | 99560 | 99573 | 99585 | 99598 | 99609 | 99621 | 99632 | 99643 |
| 2,7 | 99653 | 99664 | 99674 | 99683 | 99693 | 99702 | 99711 | 99720 | 99728 | 99736 |
| 2,8 | 99744 | 99752 | 99760 | 99767 | 99774 | 99781 | 99788 | 99795 | 99801 | 99807 |
| 2,9 | 99813 | 99819 | 99825 | 99831 | 99836 | 99841 | 99846 | 99851 | 99856 | 99861 |
| 3,0 | 99865 | 99869 | 99874 | 99878 | 99882 | 99886 | 99889 | 99893 | 99896 | 99900 |
| 3,1 | 99903 | 99906 | 99910 | 99913 | 99916 | 99918 | 99921 | 99924 | 99926 | 99929 |
| 3,2 | 99931 | 99934 | 99936 | 99938 | 99940 | 99942 | 99944 | 99946 | 99948 | 99950 |
| 3,3 | 99952 | 99953 | 99955 | 99957 | 99958 | 99960 | 99961 | 99962 | 99964 | 99965 |
| 3,4 | 99966 | 99968 | 99969 | 99970 | 99971 | 99972 | 99973 | 99974 | 99975 | 99976 |
| 3,5 | 99977 | 99978 | 99978 | 99979 | 99980 | 99981 | 99981 | 99982 | 99983 | 99983 |
| 3,6 | 99984 | 99985 | 99985 | 99986 | 99986 | 99987 | 99987 | 99988 | 99988 | 99989 |
| 3,7 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 |
| 3,8 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 | 99999 |
| 3,9 | 100000 | 100000 | 100000 | 100000 | 100000 | 100000 | 100000 | 100000 | 100000 | 100000 |
On dispose des relations simples suivantes entre
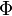
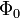
- si
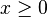
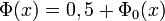
- si
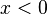
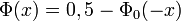
Soit T une variable aléatoire suivant la loi normale centrée réduite :
- pour tout
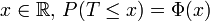
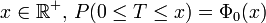
- pour tout couple
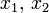
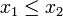
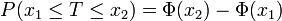
Exemples numériques
À l'aide de la table ci-dessus, on obtient, pour la variable aléatoire précédente :
![x \in\, ]-\infty;+\infty[\!](https://static.techno-science.net/illustration/Definitions/autres/3/3eb0804398728ee2cfdc3385ba9e57d7_7999a6c55d4e42384f75e1f7a03f008a.png)