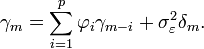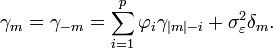Arma - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En statistiques, les modèles ARMA (modèles autorégressifs et moyenne mobile), ou aussi modèle de Box-Jenkins, sont les principaux modèles de séries temporelles.
Étant donné une série temporelle Xt, le modèle ARMA est un outil pour comprendre et prédire, éventuellement, les valeurs futures de cette série. Le modèle est composé de deux parties : une part autorégressive (AR) et une part moyenne-mobile (MA). Le modèle est généralement noté ARMA(p,q), où p est l'ordre de la partie AR et q l'ordre de la partie MA.
Modèle autorégressif
La notation AR(p) réfère au modèle autorégressif d'ordre p. Le modèle AR(p) se note
où
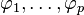
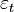
Des contraintes supplémentaires sur les paramètres sont nécessaires pour garantir la stationnarité. Par exemple, pour le modèle AR(1), les processus tels que |φ1| ≥ 1 ne sont pas stationnaires.
Exemple : un processus AR(1)
Un modèle AR(1) est donné par :
où
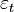
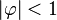
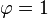
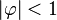
Ainsi
En particulier, prendre c = 0 revient à avoir une moyenne nulle.
La variance vaut
La fonction d'autocovariance se donne par
On peut voir que la fonction d'autocovariance décroît avec un taux de
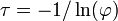
La densité spectrale de puissance est la transformée de Fourier de la fonction d'autocovariance. Dans le cas discret, cela s'écrit :
Ce développement est périodique dû à la présence du terme en cosinus au dénominateur. En supposant que le temps d'échantillonnage (Δt = 1) est plus petit que le decay time (τ), alors on peut utiliser une approximation continue de Bn :
qui présente une forme lorentzienne pour la densité spectrale :
où γ = 1 / τ est la fréquence angulaire associée à τ.
Une expression alternative pour Xt peut être dérivée en substituant Xt − 1 par
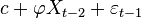
Pour N devenant très grand,
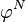
On peut voir que Xt est le bruit blanc convolé avec le noyau
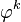

Estimation des paramètres AR
Le modèle AR(p) est donné par
Les paramètres à estimer sont
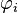
où m = 0, ... , p, ce qui donne en tout p + 1 équations. Les coefficients γm est la fonction d'autocorrélation de X,
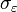
La dernière partie de l'équation est non-nulle si m = 0 ; en prenant m > 0, l'équation précédente s'écrit comme un système matriciel
Pour m = 0, nous avons
qui permet de trouver
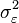
Les équations de Yule-Walker procurent un moyen d'estimer les paramètres du modèle AR(p), en remplaçant les covariances théoriques par des valeurs estimées. Une manière d'obtenir ces valeurs est de considérer la régression linéaire de Xt sur ses p premiers retards.
Obtention des équations de Yule-Walker
L'équation définissante du processus AR est
En multipliant les deux membres par Xt − m et en prenant l'espérance, on obtient
Or, il se trouve que E[XtXt − m] = γm par définition de la fonction d'autocorrélation. Les termes du bruit blancs sont indépendants les uns des autres et, de plus, Xt − m est indépendant de εt où m est plus grand que zéro. Pour m > 0, E[εtXt − m] = 0. Pour m = 0,
Maintenant, on a pour m ≥ 0,
Par ailleurs,
qui donne les équations de Yule-Walker :
pour m ≥ 0. Pour m < 0,
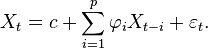
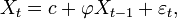
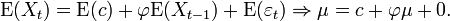
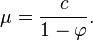
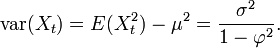
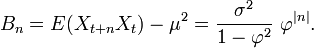
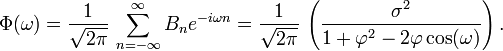
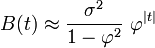
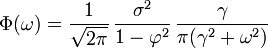
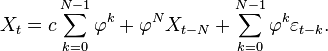
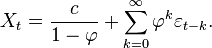
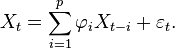
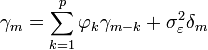
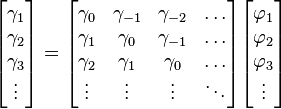
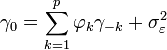
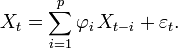
![E[X_t X_{t-m}] = E\left[\sum_{i=1}^p \varphi_i\,X_{t-i} X_{t-m}\right]+ E[\varepsilon_t X_{t-m}].](https://static.techno-science.net/illustration/Definitions/autres/e/e7af63255d6a74334e8d34b666777037_1ed5cc1b9a63ef321919f419624281d7.png)
![E[\varepsilon_t X_{t}] = E\left[\varepsilon_t \left(\sum_{i=1}^p \varphi_i\,X_{t-i}+ \varepsilon_t\right)\right] = \sum_{i=1}^p \varphi_i\, E[\varepsilon_t\,X_{t-i}] + E[\varepsilon_t^2] = 0 + \sigma_\varepsilon^2,](https://static.techno-science.net/illustration/Definitions/autres/8/88d3b15dfb38be4b18970c036c4348d1_ba572d8814d88ee5d5ef5e3be78657a5.png)
![\gamma_m = E\left[\sum_{i=1}^p \varphi_i\,X_{t-i} X_{t-m}\right] + \sigma_\varepsilon^2 \delta_m.](https://static.techno-science.net/illustration/Definitions/autres/3/395b5327bd07ef1a26a86378b711ffb9_badbdfe6d301690757bb3e8ae8cb386f.png)
![E\left[\sum_{i=1}^p \varphi_i\,X_{t-i} X_{t-m}\right] = \sum_{i=1}^p \varphi_i\,E[X_{t} X_{t-m+i}] = \sum_{i=1}^p \varphi_i\,\gamma_{m-i},](https://static.techno-science.net/illustration/Definitions/autres/f/f1ec9d209d59a1cfe284e284d83c6a59_bbcf98d44730f0580e647560a664c6a4.png)