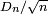Bijection de Joyal - Définition
La liste des auteurs de cet article est disponible ici.
Correspondance de Foata
L'ensemble C des éléments cycliques de ƒ est le plus grand sous-ensemble de
![\scriptstyle\ [\![1,n]\!]](https://static.techno-science.net/illustration/Definitions/autres/4/4f7c2145ef89507b6795bb90369c150f_37b9a339e0652aec7caa1e9ca41d021e.png)
- la restriction de ƒ à C est une bijection de C dans C.
On peut alors appliquer la correspondance de Foata à la restriction de ƒ à C, que nous noterons τ, et obtenir ainsi un arrangement (une suite ordonnée) ω de tous les éléments de C. La correspondance de Foata consiste à écrire la suite des cycles de la décomposition en cycles disjoints de τ, en prenant bien soin :
- de terminer chacun de ces cycles par son plus petit élément,
- d'écrire les dits cycles dans l'ordre croissant de leurs plus petits éléments.
Le premier et le dernier terme de l'arrangement ω ainsi obtenu sont destinés à être les deux sommets marqués de l'arbre de Cayley produit, à partir de ƒ, par la bijection de Joyal.
Distance entre deux points au hasard d'un arbre de Cayley aléatoire
Comme autre application, on peut citer le calcul de la loi de la distance
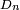
![\scriptstyle\ [\![1,n]\!]](https://static.techno-science.net/illustration/Definitions/autres/4/4f7c2145ef89507b6795bb90369c150f_37b9a339e0652aec7caa1e9ca41d021e.png)
![\scriptstyle\ [\![1,n]\!]](https://static.techno-science.net/illustration/Definitions/autres/4/4f7c2145ef89507b6795bb90369c150f_37b9a339e0652aec7caa1e9ca41d021e.png)
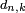
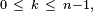
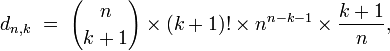
où
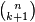
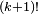
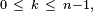
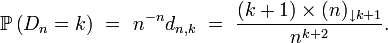
Cette loi discrète apparaît aussi dans des problèmes d'allocations (boules et urnes), dont le fameux problème des anniversaires. On peut montrer, par exemple à l'aide du lemme de Scheffé, que