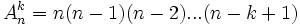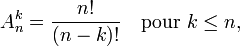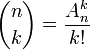Arrangement - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La notion d'arrangement est utilisée en probabilités, et notamment pour les dénombrements en analyse combinatoire.
En mathématiques, lorsque nous choisissons k objets parmi n objets discernables et que l’ordre dans lequel les objets sont sélectionnés revêt une importance, nous pouvons les représenter par un k-uplet d'éléments distincts et on en constitue une liste ordonnée sans répétition possible, c'est-à-dire dans laquelle l'ordre des éléments est pris en compte (si l'on permute deux éléments de la liste, on a une liste différente, et un élément ne peut être présent qu'une seule fois).
Une telle liste ordonnée est appelée un arrangement. Le nombre d'arrangements que l'on peut faire est noté
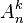
Cette formule peut se comprendre à l'aide d'un arbre des choix successifs, puisque le premier élément est choisi parmi n, le second parmi (n-1) ... et le dernier parmi (n-k+1). Avec la notation factorielle, où n! = 1×2×...n, cette formule devient
pendant que
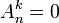
Akn est en fait le nombre d'injections que l'on peut faire d'un ensemble à k éléments vers un ensemble à n éléments. Le nombre d'arrangements est lié au coefficient binomial
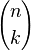
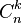
Exemple : À un examen, cinq candidats tirent les uns après les autres un sujet dans une urne contenant des questions toutes différentes. Le premier tirage se fera sur un ensemble de 50 questions possibles. À chaque tirage suivant, la question qui vient d'être tirée est enlevée de l'urne. Ainsi, en faisant passer les cinq candidats, le tirage se fait d'abord sur 50, puis sur 49, et ainsi de suite jusqu'à 46 qui représente l'ensemble des questions restantes dans l'urne pour le dernier tirage. L'arrangement va consister à additioner à chaque modification possible de cet ensemble de départ la nouvelle probabilité de piocher une question donnée. La solution pour cet exemple est donc un arrangement de 5 (k) à 50 (n).
Si on remettait la question tirée de nouveau dans l'urne à chaque tirage, ce serait un arrangement avec répétition de 5 (k) à 50 (n), et la solution vaudrait 50^5.
Exemples d'arrangements :
- une phrase sans répétition de mot est un arrangement du dictionnaire ;
- une association forme son bureau (président, trésorier, secrétaire) à partir des membres de l'association ; le bureau est un arrangement de l'association ;
- le podium d'une course est un arrangement de l'ensemble des participants.
Définition mathématique
- Définition
Soient E un ensemble fini de cardinal n et k un entier naturel. Un k-arrangement sans répétition de E est une application injective de {1, 2, ..., k} dans E.
- Autre définition
Soient E un ensemble fini de cardinal n et k un entier naturel. Un k-arrangement de E (ou k-arrangement sans répétition de E, ou encore arrangement sans répétition de n éléments pris k à k) est un k-uplet (a1, a2, ..., ak) d'éléments de E tel que ai≠aj qqsoit i, j € [1,k] avec i≠j, . Un tel k-uplet est aussi appelé k-liste distincte d'éléments de E.
- Théorème
Soient E et F deux ensembles finis de cardinaux respectifs n et k. L’ensemble
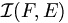
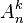
- Démonstration
- Si k > n, alors il n'existe aucune injection de F dans E et donc
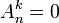
- Si k < n, alors démontrons l'égalité par récurrence sur l'entier k.
- Si k = 1 alors F est un singleton et toute application de F dans E est injective donc
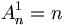
- Supposons l'égalité vérifiée pour tout ensemble F de cardinal k - 1 (2 ≤ k ≤ n) et démontrons la au rang k :
Soit F un ensemble de cardinal k, et x un élément de F. Posons G=F\{x}. Nous avons card(G)=k-1.
Considérons la relation qui relie deux injections de F dans E quand elles ont même restriction à G. Les classes d'équivalence partitionnent
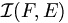
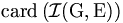
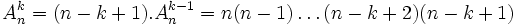
- Si k = 1 alors F est un singleton et toute application de F dans E est injective donc
- Si k=0, nous poserons par convention pour tout entier naturel n
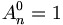
- Démonstration (élémentaire)
Si 1 ≤ k ≤ n alors supposons que F={x1, x2, ..., xk}. Pour construire une application injective de F dans E, nous devons
- choisir l'image de x1 et il y a n images possibles,
- choisir l'image de x2 et il reste n-1 images possibles,
- ...
- choisir l'image de xk, il reste dans l'ensemble E n - (k-1) éléments non atteints donc n - (k-1) images possibles.
Au total, nous avons construit n.(n-1).....(n - k + 1) applications injectives différentes.
- Corollaire
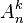

- Démonstration
Supposons F={x1, x2, ..., xk}. Une injection f de F dans E s'identifie au k-uplet d'éléments distincts (f(x1), f(x2), ..., f(xk)). Il y a donc une bijection entre l'ensemble des applications injectives de F dans E et l'ensemble des k-uplets d'éléments distincts de E.
- Remarque
Construire un arrangement revient à placer les uns après les autres, k objets discernables pris parmi n, dans k cases numérotées et donc une permutation de n éléments est un n-arrangement de n éléments. La notion d'arrangement généralise donc celle de permutation.