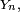Samedi 26 Avril 2025
Rechercher 🔍

Lemme de Scheffé - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Énoncé et démonstration - A voir - Variante discrète

Introduction

Le lemme de Scheffé est un critère de convergence en loi concernant les suites de variables aléatoires à densité.

Énoncé et démonstration

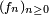
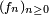
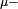
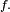
Lemme de Scheffé —  Soit \scriptstyle\ (f_{n})_{n\ge 0}\ une suite de densités de probabilité définies sur le même espace \scriptstyle\ E\ et par rapport à la même mesure \scriptstyle\ \mu\ sur \scriptstyle\ E\ . Supposons que \scriptstyle\ (f_{n})_{n\ge 0}\ converge \scriptstyle\ \mu-\ presque partout vers une densité de probabilité \scriptstyle\ f.\ Alors

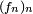
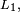
  • \scriptstyle\ (f_{n})_{n}\ converge vers \scriptstyle\ f\ dans \scriptstyle\ L_{1},\
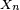
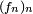
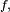
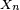
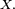
  • si les variables aléatoires \scriptstyle\ X_{n}\ et \scriptstyle\ X\ ont pour densités respectives \scriptstyle\ (f_{n})_{n}\ et \scriptstyle\ f,\ alors \scriptstyle\ X_{n}\ converge en loi vers \scriptstyle\ X.\

On a

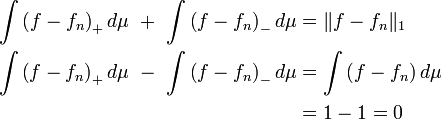
\begin{align} \int\left(f-f_{n}\right)_{+}d\mu\ +\ \int\left(f-f_{n}\right)_{-}d\mu &= \Vert f-f_{n}\Vert_{1} \\ \int\left(f-f_{n}\right)_{+}d\mu\ -\ \int\left(f-f_{n}\right)_{-}d\mu &= \int\left(f-f_{n}\right)d\mu \\ &= 1-1=0 \end{align}

Mais

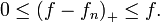
0 \le \left(f-f_{n}\right)_{+} \le f.

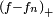
Or \scriptstyle\ f\ est intégrable, et, par hypothèse, \scriptstyle\ \left(f-f_{n}\right)_{+}\ converge vers 0 \scriptstyle\ \mu\ -p.p., ce qui permet de conclure, à l'aide du théorème de convergence dominée, que

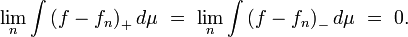
\lim_n\int\left(f-f_{n}\right)_{+}d\mu\ =\ \lim_n\int\left(f-f_{n}\right)_{-}d\mu\ =\ 0.

En conséquence,

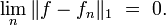
\lim_n\Vert f-f_{n}\Vert_{1}\ =\ 0.

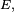
De plus, notons que pour \scriptstyle\ \varphi\ continue bornée sur \scriptstyle\ E,\ on a

\begin{align} \left|\mathbb{E}[\varphi(X_{n})]-\mathbb{E}[\varphi(X)]\right|&= \left|\int_{E}\varphi f_{n}d\mu-\int_{E}\varphi fd\mu\right| \\ &\le \Vert \varphi\Vert_{\infty}\Vert f_{n}-f\Vert_{1}. \end{align}

Par suite

\lim_n\mathbb{E}[\varphi(X_{n})] =\ \mathbb{E}[\varphi(X)],

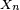
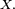
ce qui caractérise bien la convergence en loi de \scriptstyle\ X_{n}\ vers \scriptstyle\ X.\

Donc, lorsque des fonctions sont positives et ont la même intégrale, on est affranchi des hypothèses habituelles de majoration uniforme de l'erreur apparaissant dans le théorème de convergence dominée.

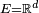
En général, on applique le lemme de Scheffé dans le cas où \scriptstyle\ E=\mathbb{R}^d\ et où la mesure \scriptstyle\ \mu\ est la mesure de Lebesgue : les variables aléatoires apparaissant dans le lemme sont alors des variables "à densité".

Exemple : convergence de la loi de Student vers la loi normale

Un exemple d'application est la convergence de la loi de Student vers la loi normale. Pour k ≥ 1, la loi de Student à k degrés de liberté a pour densité

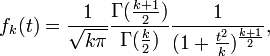
f_k(t)=\frac{1}{\sqrt{k\pi}}\frac{\Gamma(\frac{k+1}{2})}{\Gamma(\frac{k}{2})}\frac{1}{(1+\frac{t^2}{k})^{\frac{k+1}{2}}},

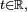
où Γ désigne la fonction Gamma d'Euler. On a classiquement, pour tout \scriptstyle\ t\in\mathbb{R},

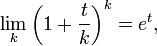
\lim_k\left(1+\frac{t}{k}\right)^{k}=e^{t},

et donc

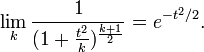
\lim_k\frac{1}{(1+\frac{t^2}{k})^{\frac{k+1}{2}}}=e^{-t^2/2}.

On a aussi

\lim_{t\uparrow+\infty}\frac{\Gamma(t+\frac{1}{2})}{\Gamma(t)\sqrt{t}}=1.

Donc

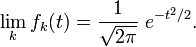
\lim_kf_k(t)=\frac{1}{\sqrt{2\pi}}\ e^{-t^2/2}.

CQFD

A voir

Bibliographie

  • (en) Rick Durrett, Probability : Theory and Examples, Thomson Brooks/Cole (Belmont, CA), coll. « Duxbury advanced series », 2005, 3e éd., 497 p.  , Section II.2.a., page 81.

Pages liées

Variante discrète

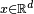
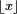
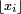
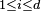
Sous certaines conditions, on peut adapter le lemme de Scheffé pour démontrer la convergence de lois discrètes vers des lois à densité. Pour un vecteur \scriptstyle\ x\in\mathbb{R}^d , notons \scriptstyle\ \left\lfloor x\right\rfloor\ le vecteur de coordonnées \scriptstyle\ \left\lfloor x_{i}\right\rfloor\ , \scriptstyle\ 1\le i\le d . Alors

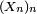
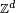
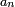
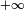
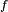
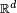
Lemme de Scheffé discret —  On se donne une suite de v.a. \scriptstyle\ (X_{n})_{n}\ à valeurs dans \scriptstyle\ \mathbb{Z}^d , une suite \scriptstyle\ a_{n} , tendant vers \scriptstyle\ +\infty , de réels strictement positifs, et une densité de probabilité \scriptstyle\ f sur \scriptstyle\ \mathbb{R}^d . Si p.p. en \scriptstyle\ x on a

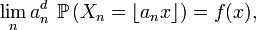
\lim_{n} a_{n}^d\ \mathbb{P}\left(X_{n}=\left\lfloor a_{n}x\right\rfloor \right)=f(x),

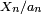
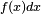
alors \scriptstyle\ X_{n}/a_{n} converge faiblement vers \scriptstyle\ f(x) dx .

Considérons la fonction

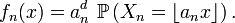
f_{n}(x) = a_{n}^d\ \mathbb{P}\left(X_{n}=\left\lfloor a_{n}x\right\rfloor\right).

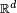
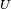
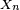
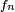
C'est une densité de probabilité par rapport à la mesure de Lebesgue (notée \scriptstyle\ \mu ) sur \scriptstyle\ \mathbb{R}^d . Par exemple, si \scriptstyle\ U est une variable aléatoire de loi uniforme sur \scriptstyle\ [0,1]^d , indépendante de \scriptstyle\ X_{n} , alors \scriptstyle\ f_{n} est la densité de

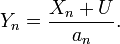
Y_{n} = \frac{X_{n}+U}{a_{n}}.

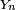
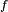
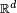
Le lemme de Scheffé ordinaire montre que \scriptstyle\ Y_{n} converge en loi vers \scriptstyle\ f . Mais, pour n'importe quelle norme sur \scriptstyle\ \mathbb{R}^d ,

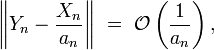
\left\Vert Y_{n}-\frac{X_{n}}{a_{n}}\right\Vert\ =\ \mathcal{O}\left( \frac1{a_{n}}\right),

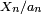
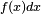
donc, en vertu du théorème de Slutsky, \scriptstyle\ X_{n}/a_{n} aussi converge faiblement vers \scriptstyle\ f(x) dx .

Une fois cette dernière démonstration faite, le lemme de Scheffé discret dispense de trouver une majoration du terme d'erreur

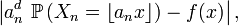
\left|a_{n}^d\ \mathbb{P}\left(X_{n}=\left\lfloor a_{n}x\right\rfloor \right)-f(x)\right|,

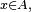
uniforme pour \scriptstyle\ x\in A, ce qui serait une manière plus lourde de montrer que

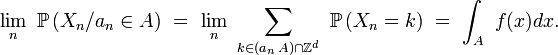
\lim_n\ \mathbb{P}\left(X_{n}/a_n \in A \right)\ =\ \lim_n\ \sum_{k\in(a_n\,A)\cap\mathbb{Z}^d}\ \mathbb{P}\left(X_{n}=k \right)\ =\ \int_A\ f(x)dx.

Habituellement, un contrôle uniforme de la rapidité de convergence des termes de la somme est nécessaire pour assurer la convergence du terme de gauche de l'égalité (le terme de gauche est une somme finie dont le nombre de termes tend vers l'infini) vers l'intégrale limite. Dans ce cas précis, grâce au lemme de Scheffé, la convergence des termes de la somme, renormalisés, suffit pour assurer la convergence du terme de gauche de l'égalité.

Distance entre deux points au hasard d'un arbre de Cayley aléatoire

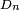
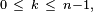
La loi de la distance \scriptstyle\ D_n entre deux points au hasard d'un arbre de Cayley aléatoire, est donnée, pour \scriptstyle\ 0\ \le\ k\ \le\ n-1,\ par

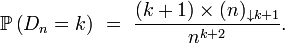
\mathbb{P}\left(D_n=k\right)\ =\ \frac{(k+1)\times(n)_{\downarrow k+1}}{n^{k+2}}.

En vertu de la bijection de Joyal, c'est aussi la loi du nombre de points cycliques d'une application de \scriptstyle\ [\![1,n]\!] dans \scriptstyle\ [\![1,n]\!].\ Cette loi discrète apparaît aussi dans des problèmes d'allocations (boules et urnes), dont le fameux problème des anniversaires. 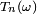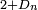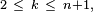Lorsqu'on alloue séquentiellement des boules dans un ensemble de n urnes, avec équiprobabilité, ce qui revient à considérer un univers probabiliste \scriptstyle\ \Omega\ =\ [\![1,n]\!]^{\mathbb{N}},\ le rang \scriptstyle\ T_n(\omega)\ de la première boule à être allouée dans une urne non vide suit la même loi que \scriptstyle\ 2+D_n\  : pour \scriptstyle\ 2\ \le\ k\ \le\ n+1,\

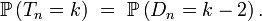
\mathbb{P}\left(T_n=k\right)\ =\ \mathbb{P}\left(D_n=k-2\right).

On peut montrer, à l'aide du lemme de Scheffé, que

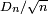
Proposition —  \scriptstyle\ D_n/\sqrt{n} converge en loi vers la loi de Rayleigh.

En effet, pour un nombre réel x strictement positif,

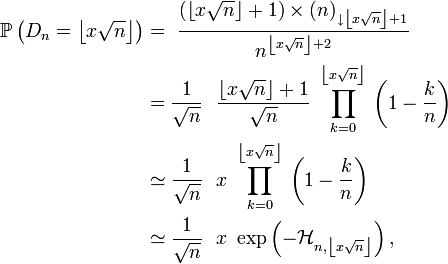
\begin{align} \mathbb{P}\left(D_n=\left\lfloor x\sqrt{n}\right\rfloor\right) &=\ \frac{(\left\lfloor x\sqrt{n}\right\rfloor+1)\times(n)_{\downarrow \left\lfloor x\sqrt{n}\right\rfloor+1}}{n^{\left\lfloor x\sqrt{n}\right\rfloor+2}}\\ &=\frac{1}{\sqrt{n}}\ \ \frac{\left\lfloor x\sqrt{n}\right\rfloor+1}{\sqrt{n}}\ \prod_{k=0}^{\left\lfloor x\sqrt{n}\right\rfloor}\,\left(1-\frac{k}{n}\right)\\ &\simeq\frac{1}{\sqrt{n}}\ \ x\ \prod_{k=0}^{\left\lfloor x\sqrt{n}\right\rfloor}\,\left(1-\frac{k}{n}\right)\\ &\simeq\frac{1}{\sqrt{n}}\ \ x\ \exp\left(-\mathcal{H}_{n,\left\lfloor x\sqrt{n}\right\rfloor}\right), \end{align}

où

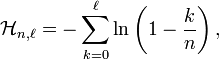
\mathcal{H}_{n,\ell}=-\sum_{k=0}^{\ell}\ln\left(1-\frac{k}{n}\right),

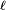
et pour \scriptstyle\ \ell\ suffisamment petit,

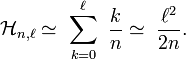
\mathcal{H}_{n,\ell}\simeq\ \sum_{k=0}^{\ell}\ \frac{k}{n}\simeq\ \frac{\ell^2}{2n}.

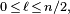
Plus précisément, pour \scriptstyle\ 0\,\le\,\ell\,\le\,n/2,\

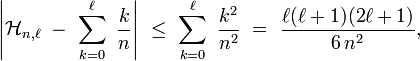
\left|\mathcal{H}_{n,\ell}\ -\ \sum_{k=0}^{\ell}\ \frac{k}{n}\right|\ \le\ \sum_{k=0}^{\ell}\ \frac{k^2}{n^2}\ =\ \frac{\ell(\ell+1)(2\ell+1)}{6\,n^2},

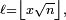
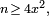
et pour \scriptstyle\ \ell=\left\lfloor x\sqrt{n}\right\rfloor,\ dès que \scriptstyle\ n\,\ge\,4x^2,\

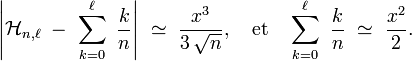
\left|\mathcal{H}_{n,\ell}\ -\ \sum_{k=0}^{\ell}\ \frac{k}{n}\right|\ \simeq\ \frac{x^3}{3\,\sqrt{n}},\quad\text{et}\quad\sum_{k=0}^{\ell}\ \frac{k}{n}\ \simeq\ \frac{x^2}{2}.

Ainsi, pour tout nombre réel x strictement positif,

CQFD

En conséquence :

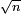
  • la distance "typique" entre deux points d'un arbre de taille n est de l'ordre de \scriptstyle\ \sqrt{n}\ ;
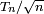
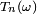
  • \scriptstyle\ T_n/\sqrt{n} converge en loi vers la loi de Rayleigh. 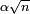Dans le cadre du problème des anniversaires, où l'on choisit n=365, \scriptstyle\ T_n(\omega)\ s'interprète comme la taille du groupe pour laquelle il devient probable qu'au moins deux membres du groupe ait la même date d'anniversaire (il faut imaginer un groupe dont l'effectif augmente progressivement)  : la probabilité que dans un groupe de \scriptstyle\ \alpha\sqrt{n}\ personnes, toutes les dates d'anniversaire soit différentes, peut être estimée comme suit :
\mathbb{P}\left(T_n>\alpha\sqrt{n}\right)=\mathbb{P}\left(T_n/\sqrt{n}\ >\alpha\right)\simeq\int_{\alpha}^{+\infty}x\ \exp\left(-x^2/2\right)dx\ =\ e^{-\alpha^2/2},
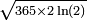
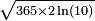
et vaut donc 1/2 pour un groupe d'approximativement \scriptstyle\ \sqrt{365\times2\ln(2)}\ (soit 22,5) personnes, ou bien 1/10 pour un groupe d'approximativement \scriptstyle\ \sqrt{365\times2\ln(10)}\ (soit 41) personnes. Le calcul exact du premier entier tel que cette probabilité soit plus petite que 1/2 (respectivement 1/10) donne les mêmes résultats : 23 (respectivement 41).

Un contrexemple : la marche aléatoire simple symétrique

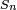
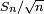
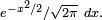
Notons \scriptstyle\ S_{n} la position de la marche aléatoire simple symétrique au temps \scriptstyle\ n . Abraham De Moivre a montré que \scriptstyle\ S_{n}/\sqrt n converge en loi vers \scriptstyle\ e^{-x^2/2}/\sqrt{2\pi}\ dx.\ Ce faisant, Abraham De Moivre a mis à son compte 3 « premières » :

  • première apparition de la loi normale,
  • première version du théorème de la limite centrale,
  • découverte et première utilisation de la formule de Stirling.

Malheureusement, on ne peut pas appliquer directement le lemme de Scheffé discret pour prouver le résultat de De Moivre. En effet :

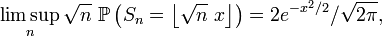
\limsup_{n} \sqrt{n}\ \mathbb{P}\left(S_{n}=\left\lfloor \sqrt{n}\ x\right\rfloor \right)=2e^{-x^2/2}/\sqrt{2\pi},

et

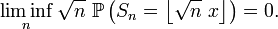
\liminf_{n} \sqrt{n}\ \mathbb{P}\left(S_{n}=\left\lfloor \sqrt{n}\ x\right\rfloor \right)=0.

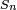
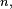
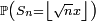
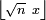
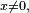
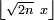
Comme \scriptstyle\ S_{n} est de même parité que \scriptstyle\ n, la suite \scriptstyle\ \mathbb{P}\left(S_{n}=\left\lfloor \sqrt{n}x\right\rfloor \right)\ prend la valeur zero pour une infinité d'indices, ceux pour lesquels \scriptstyle\ \left\lfloor \sqrt{n}\ x\right\rfloor et \scriptstyle\ n\ n'ont pas la même parité : dès que \scriptstyle\ x\neq 0, on peut vérifier à la main que \scriptstyle\ \left\lfloor \sqrt{2n}\ x\right\rfloor est impair pour une infinité d'indices (et pair pour une infinité d'indices également), un constat analogue pouvant être fait pour \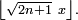scriptstyle\ \left\lfloor \sqrt{2n+1}\ x\right\rfloor. 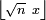En revanche, lorsque \scriptstyle\ \left\lfloor \sqrt{n}\ x\right\rfloor et \scriptstyle\ n\ ont même parité, on a:

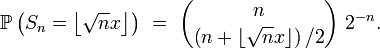
\mathbb{P}\left(S_{n}=\left\lfloor \sqrt{n}x\right\rfloor \right)\ =\ {n\choose \left(n+\left\lfloor \sqrt{n}x\right\rfloor\right)/2}\ 2^{-n}.

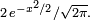
La formule de Stirling conduit alors à la limite annoncée, \scriptstyle\ 2\,e^{-x^2/2}/\sqrt{2\pi}.\ On peut cependant adapter la démonstration du lemme de Scheffé discret à ce cas particulier : il suffit de poser

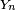
Alors \scriptstyle\ Y_{n}\ a pour densité

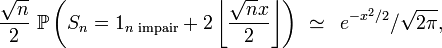
\frac{\sqrt{n}}2\ \mathbb{P}\left(S_{n}=1_{n\text{ impair}}+2\left\lfloor \frac{\sqrt{n}x}2\right\rfloor \right)\ \simeq\ \,e^{-x^2/2}/\sqrt{2\pi},

toujours via la formule de Stirling. Ainsi \scriptstyle\ Y_{n}\ converge en loi vers la loi normale, en vertu du lemme de Scheffé. Mais, comme plus haut,

\left\Vert Y_{n}-\frac{S_{n}}{\sqrt{n}}\right\Vert\ =\ \mathcal{O}\left( \frac1{\sqrt{n}}\right).

Le théorème de de Moivre résulte alors de la convergence en loi de \scriptstyle\ Y_{n},\ et du théorème de Slutsky.

- Introduction - Énoncé et démonstration - A voir - Variante discrète
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
miniature
Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️
miniature
Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜
miniature
Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️
miniature
Cette vitamine développe les fonctions cognitives du cerveau 🧠
miniature
Comment des impacts géants vaporisent les corps planétaires ☄️
miniature
Les Américains riches vivent moins longtemps que les Européens pauvres 💰
miniature
Attention à ce riz naturellement riche en arsenic 🍚
miniature
L'intelligence artificielle contre la mort subite 💀
miniature
L'inévitable formation d'un océan de magma basal sur Terre 🔥
miniature
Découverte d'une plante étrange sans chlorophylle 🌱
miniature
Existe-t-il des mélodies naturelles ? 🎶
miniature
Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽
miniature
L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡
miniature
1
Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺
miniature
Imprimer en 3D avec la lumière du soleil ☀️
miniature
La pollution atmosphérique nuit gravement au cerveau 🧠
miniature
Le trou noir supermassif Ansky vient de se réveiller ⚫
miniature
1
Voici ce qui rend notre cerveau vraiment unique 🧠
miniature
Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩
miniature
Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬
miniature
La physique révèle les secrets d'un strike parfait au bowling 🎳
miniature
Le TDAH associé à la démence 🧠
miniature
Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️
miniature
Le régime cétogène montre des surprises sur le cholestérol 🧐
miniature
Un tango observationnel révèle une Super-Terre 🔭
miniature
Cette expérience montre que la graisse brune augmente fortement la longévité 🕒
Page générée en 0.178 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise