Bijection de Joyal - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La bijection de Joyal consiste à "déplier", à l'aide de la correspondance fondamentale de Foata, la partie cyclique d'une application de
![\scriptstyle\ [\![1,n]\!]](https://static.techno-science.net/illustration/Definitions/autres/4/4f7c2145ef89507b6795bb90369c150f_37b9a339e0652aec7caa1e9ca41d021e.png)
![\scriptstyle\ [\![1,n]\!],\](https://static.techno-science.net/illustration/Definitions/autres/2/2a651eaac1411f8cb9b4d790e1119ff6_411f5961813d943723430c8295bc9bde.png)
La bijection de Joyal est aussi très utile pour l'étude des propriétés métriques des arbres étiquetés à n sommets.
Une application : une démonstration de la formule de Cayley
Notons
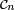
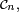
![\scriptstyle\ [\![1,n]\!]](https://static.techno-science.net/illustration/Definitions/autres/4/4f7c2145ef89507b6795bb90369c150f_37b9a339e0652aec7caa1e9ca41d021e.png)
![\scriptstyle\ [\![1,n]\!]](https://static.techno-science.net/illustration/Definitions/autres/4/4f7c2145ef89507b6795bb90369c150f_37b9a339e0652aec7caa1e9ca41d021e.png)
![\scriptstyle\ [\![1,n]\!]^{[\![1,n]\!]}](https://static.techno-science.net/illustration/Definitions/autres/c/c843515b9b1ba970cb71eddc1fcb2485_261491357ba2bcad56ba8d2ca8b69021.png)
![n^n\ =\ \text{Card}\ [\![1,n]\!]^{[\![1,n]\!]}\ =\ \text{Card}\ \left(\mathcal{C}_n\times[\![1,n]\!]^2\right)\ =\ n^2\,\text{Card}\ \mathcal{C}_n.](https://static.techno-science.net/illustration/Definitions/autres/0/0457caca9dc3918dc5bdc1791e913b35_642ee2f7459dc1f4f79145edefb35ad5.png)
Cette démonstration est attribuée à André Joyal par Aigner et Ziegler, ou encore par Pitman.
On peut voir comme l'ensemble des arbres de Cayley à n sommets, dont deux sommets sont marqués, de deux marques différentes. Le sommet portant la première marque peut être interprété comme la racine de l'arbre. Les deux marques différentes peuvent être portées par le même sommet.
La bijection de Joyal permet aussi de mieux comprendre la topologie d'un arbre de taille n, en étudiant la distance entre 2 sommets au hasard d'un arbre au hasard. En effet, un élément tiré au hasard avec équiprobabilité dans
![\scriptstyle\ \Omega = \mathcal{C}_n\times[\![1,n]\!]^2](https://static.techno-science.net/illustration/Definitions/autres/2/2e5035bafcce82c4e4980a5cc16e446c_1add1b3052ec4a1b287f8a174b2ae126.png)
![\scriptstyle\ \Omega = \mathcal{C}_n\times[\![1,n]\!]^2.\](https://static.techno-science.net/illustration/Definitions/autres/a/aca75deaea2292ea4904072f98f8b883_e3771c1cdb2bee2a143d444f3bc816f1.png)
Éléments cycliques et éléments transients
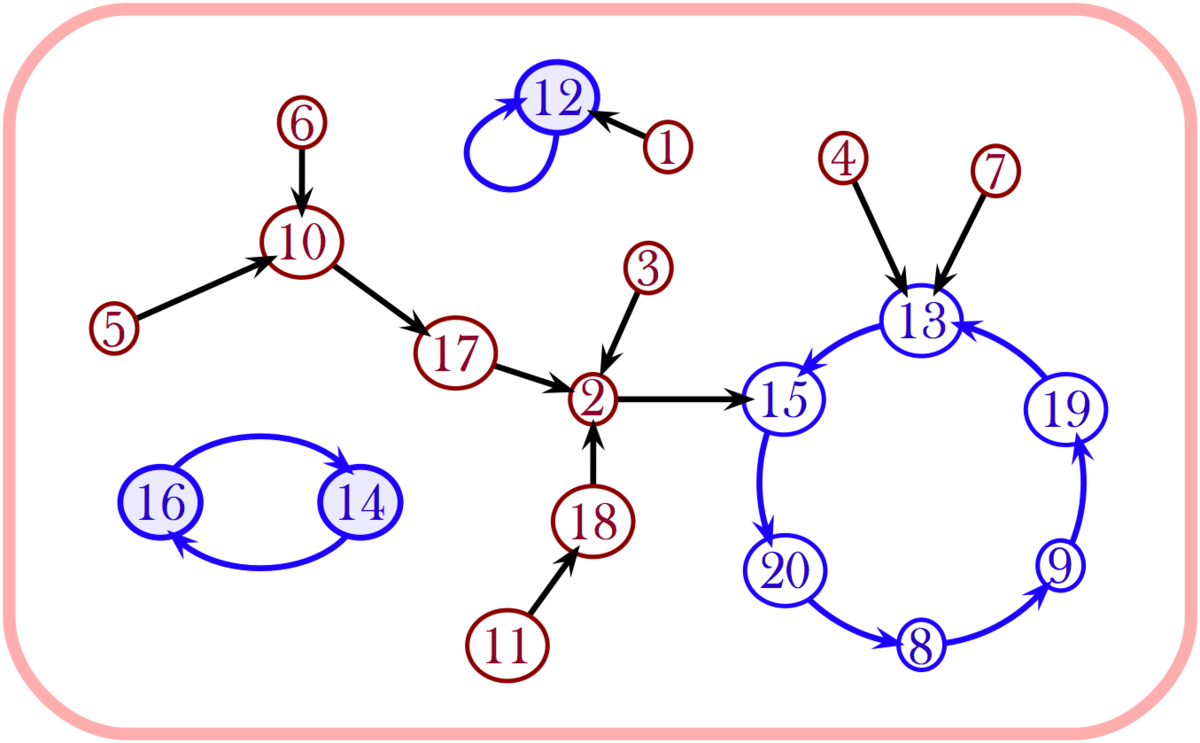
Dans l'ensemble de définition de ƒ on peut distinguer les éléments cycliques (ou récurrents) des éléments transients : les éléments cycliques, figurés ci-contre en bleu, sont les éléments x pour lesquels il existe nx > 0 tel que :
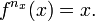
Par exemple, ci-contre, n12 = 1, n16 = 2, et n8 = 6. A chaque application ƒ de
![\scriptstyle\ [\![1,n]\!]](https://static.techno-science.net/illustration/Definitions/autres/4/4f7c2145ef89507b6795bb90369c150f_37b9a339e0652aec7caa1e9ca41d021e.png)
![\scriptstyle\ [\![1,n]\!],\](https://static.techno-science.net/illustration/Definitions/autres/2/2a651eaac1411f8cb9b4d790e1119ff6_411f5961813d943723430c8295bc9bde.png)
![p_{i,f(i)}=1,\qquad \forall i\in[\![1,n]\!].](https://static.techno-science.net/illustration/Definitions/autres/6/6163c7c2d98b2e12a965dcde008d1b70_c715758869f7d0346c51b450ef05721e.png)
Les éléments récurrents et les éléments transients de ƒ sont alors exactement les éléments récurrents et les éléments transients de cette chaîne de Markov.
Représentation graphique d'une application
Pour décrire la bijection de Joyal, il est commode d'utiliser une représentation de chaque application ƒ de
![\scriptstyle\ [\![1,n]\!]](https://static.techno-science.net/illustration/Definitions/autres/4/4f7c2145ef89507b6795bb90369c150f_37b9a339e0652aec7caa1e9ca41d021e.png)
![\scriptstyle\ [\![1,n]\!]](https://static.techno-science.net/illustration/Definitions/autres/4/4f7c2145ef89507b6795bb90369c150f_37b9a339e0652aec7caa1e9ca41d021e.png)
![\scriptstyle\ [\![1,n]\!],](https://static.techno-science.net/illustration/Definitions/autres/a/a9a29a85031aeb31fd9a259b8f085882_9ecf7f8c7115e268aadddb701351998d.png)
Bijection de Joyal
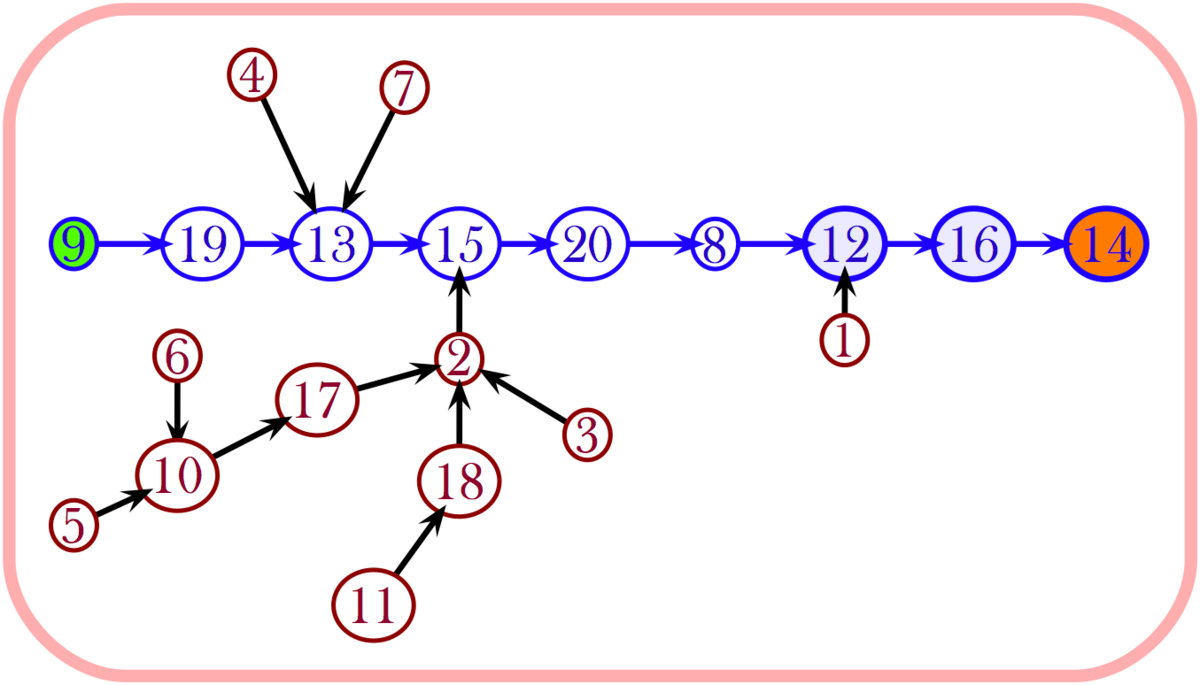
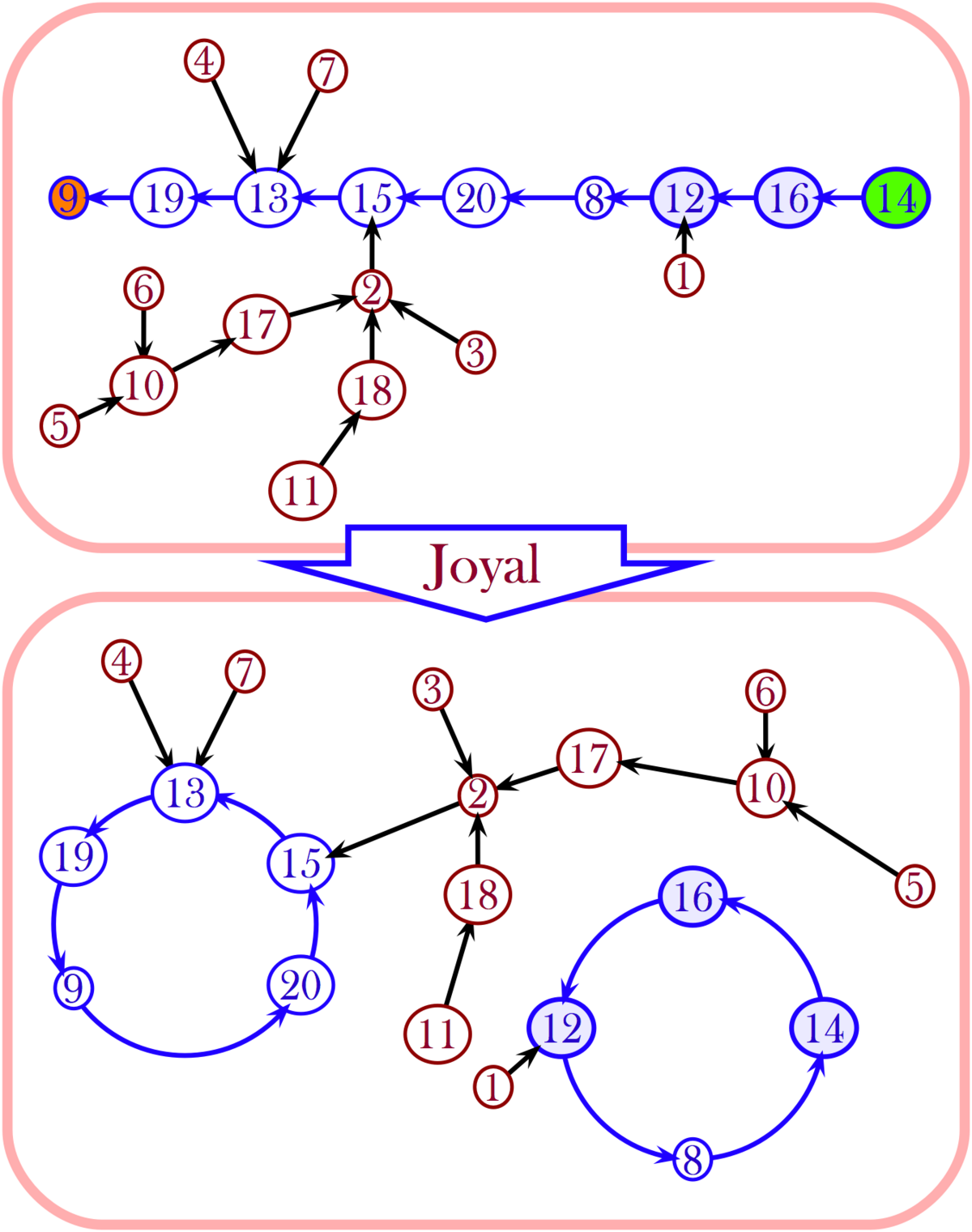
On observe qu'une fois effacées les arètes entre les éléments cycliques de ƒ, la représentation de ƒ ainsi modifiée devient une forêt (un graphe sans cycles, éventuellement non connexe, dont les composantes connexes sont précisément des arbres), chaque arbre de la forêt pouvant être vu comme enraciné en un des éléments cycliques de ƒ. En "replantant" chacun de ces arbres sur le sommet correspondant du graphe linéaire associé à l'arrangement de tous les éléments de C produit par la correspondance de Foata, on obtient un arbre de Cayley avec deux sommets marqués.
Réciproquement, la donnée d'un arbre de Cayley T avec deux points x et y marqués, éventuellement égaux, l'un marqué "début" et l'autre "fin", par exemple, définit
- une orientation de chaque arète de T (par exemple, chaque arète de T est orientée du sommet le plus éloigné de la fin (y) vers le sommet le plus proche de y) ;
- un unique chemin de longueur minimale de x à y (il existe un chemin car un arbre est un graphe connexe, il existe un seul chemin minimal car un arbre est un graphe sans cycle) ;
- une suite ordonnée de nombres de
![\scriptstyle\ [\![1,n]\!], \](https://static.techno-science.net/illustration/Definitions/autres/2/2a651eaac1411f8cb9b4d790e1119ff6_411f5961813d943723430c8295bc9bde.png)
A cette suite ω on peut appliquer la correspondance de Foata, pour trouver une permutation τ des nombres constituant ω, permutation dont le graphe est une collection de cycles. Ces cycles sont délimités par les records vers le bas de la suite obtenue en renversant la suite ω, i.e. les records observés en parcourant le chemin de y vers x.
Sur l'exemple ci-contre, x = 9 et y = 14, et le chemin minimal est ω = (9, 19, 13, 15, 20, 8, 12, 16, 14). Les records de la suite renversée (14, 16, 12, 8, 20, 15, 13, 19, 9) sont successivement 14, 12 et 8, ce qui conduit à la décomposition de τ en cycles disjoints :
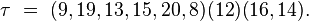
On retrouve bien ainsi les cycles de ƒ.
Une fois effacées les arètes composant le chemin de longueur minimale entre x et y, l'arbre de Cayley T ainsi modifié devient une forêt, chaque arbre de la forêt pouvant être vu comme enraciné en un des sommets du chemin entre x et y. En "replantant" chacun de ces arbres sur le sommet correspondant du graphe de τ, on obtient le graphe de ƒ.
A titre d'exemple, si l'on intervertit les rôles de x et y, on obtient un nouvel élément de
![\scriptstyle\ \mathcal{C}_n\times[\![1,n]\!]^2.\](https://static.techno-science.net/illustration/Definitions/autres/f/f2ad507b1556efbadea0f8d651ed6aae_1d5873288098afd049b29a085ac811c3.png)