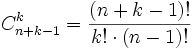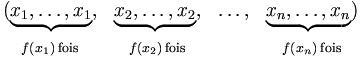Combinaison avec répétition - Définition
La liste des auteurs de cet article est disponible ici.
Une autre représentation
Soit n un entier naturel non nul, et soit l'ensemble E={x1, x2, ..., xn}. Munissons E d'une relation d'ordre total et supposons que
- x1 < x2 < ... < xn
À une k-combinaison avec répétition de E, nous associons le k-uplet croissant (au sens large)
Réciproquement à un k-uplet croissant d'éléments de E (a1, a2, ..., ak), c'est-à-dire un k-uplet tel que
- a1 < a2 < ... < ak
nous pouvons associer l'application f:E → {0, 1, ..., k} qui envoie un élément de E sur le nombre de fois où il apparaît dans le k-uplet. Il est alors évident que
- f(x1)+f(x2)+ ... +f(xn)=k
et donc que f est une k-combinaison avec répétition de E.
Ainsi, il y a une bijection entre l'ensemble des k-combinaisons avec répétition de E et l'ensemble des k-uplets croissants d'éléments de E, ou encore des applications croissantes (au sens large) de {1, 2, ..., k} dans E.
'Exemple :
Un domino peut être représenté de manière unique par un couple croissant (a, b) tel que a ⩽ b d'éléments de E={blanc, 1, 2, 3, 4, 5, 6}.
Approche moins "matheuse" des combinaisons avec répétitions
Une combinaison avec répétitions de "k" objets pris parmi "n" objets est une manière de sélectionner "k" objets parmi "n" objets distincts, sans tenir compte de l'ordre des "k" objets et avec répétitions, c’est-à-dire que le même objet peut être sélectionné plusieurs fois.
Le nombre de combinaisons avec répétitions de "k" objets pris parmi "n" objets égale :
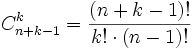
Voici deux démonstrations de cette affirmation.
Première démonstration :
Numérotons les "n" objets de 0 à (n-1).
Remarquez qu'à chaque combinaison avec répétitions de "k" objets parmi les "n", correspond une et une seule permutation avec répétitions de "n-1" boules noires et "k" boules blanches.
Le nombre de boules noires à gauche de la première boule blanche correspond au numéro d'un objet de la combinaison avec répétitions.
Le nombre de boules noires à gauche de la deuxième boule blanche correspond au numéro d'un objet de la combinaison avec répétitions.
etc. pour toutes les boules blanches.
Conclusion :
Le nombre de combinaisons avec répétitions de "k" objets pris parmi "n" objets égale le nombre de permutations avec répétitions de "k" boules blanches et de "n-1" boules noires.
Ce nombre vaut :
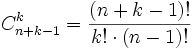
C'est le nombre de permutations des (n+k-1) boules, mais dans lesquelles on ne distingue pas les permutations des boules noires entre elles et des boules blanches entre elles.
On a (n+k-1)! permutations des boules, qu'il faut diviser par les (n-1)! permutations des boules noires et les k! permutations des boules blanches.
Deuxième démonstration :
Numérotons les "n" objets de 0 à (n-1).
Plaçons n boules noires numérotées de 0 à (n-1) et (k-1) boules blanches dans une urne.
Sur la première boule blanche est noté : "remplacez-moi par une boule noire identique à la plus à gauche".
Sur la deuxième boule blanche est noté : "remplacez-moi par une boule noire identique à la deuxième la plus à gauche".
Sur la troisième boule blanche est noté : "remplacez-moi par une boule noire identique à la troisième la plus à gauche".
etc.
On tire de l'urne "k" boules parmi les "n+k-1" boules noires et blanches. On les place par ordre des numéros sur les boules.
Le nombre de résultats possibles de l'expérience précédente est égal au nombre de combinaisons avec répétitions de "k" objets pris parmi "n" objets.
Il est également égal au nombre de combinaisons sans répétitions de "k" boules parmi les "n+k-1" boules noires et blanches.
Ce nombre est :
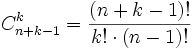
Élément d'une troisième démonstration :
Problème :
Supposons avoir un ensemble de n éléments.
Combien de sous-ensembles de k éléments peut-on construire si l’on ne tient pas compte de l’ordre, et que l’on autorise les répétitions ?
Exemple :
Prenons n = 5 et k = 3 ; { 1 ; 2 ; 3 ; 4 ; 5 } est l’ensemble des 5 éléments.
Écrivons tous les sous-ensembles non ordonnés de trois éléments de { 1 ; 2 ; 3 ; 4 ; 5 } :
| 111 122 133 144 155 | 222 233 244 255 | 333 344 355 | 444 455 | 555 |
| 112 123 134 145 | 223 234 245 | 334 345 | 445 | |
| 113 124 135 | 224 235 | 335 | ||
| 114 125 | 225 | |||
| 115 |
Pour compter ces sous-ensembles (il y en a 35 dans notre exemple !), on imagine qu’ils sont formés de combinaisons où les répétitions sont absentes.
Il faut donc trouver un moyen de transformer cette écriture...
Pour cela, on augmente de : 1 unité le chiffre des 2èmes colonnes, 2 unités le chiffre des 3èmes colonnes, ..., k-1 unités le chiffre des kèmes colonnes.
| 123 134 145 156 167 | 234 245 256 267 | 345 356 367 | 456 467 | 567 |
| 124 135 146 157 | 235 246 257 | 346 357 | 457 | |
| 125 136 147 | 236 247 | 347 | ||
| 126 137 | 237 | |||
| 127 |
Il est évident que le nombre d’éléments des deux listes est le même.
Mais la nature même des éléments a changé, puisque l’on utilise les chiffres allant de 1 à 7, et non plus de 1 à 5 comme au départ !
Notre collection de n objets est donc agrandie à n+k-1 objets.
Le nombre de combinaisons avec répétition de "k" objets pris parmi "n" est donc égale au nombre de combinaisons sans répétition de "k" objets pris parmi "n + k-1".
Ce nombre est :