Combinaison avec répétition - Définition

Une troisième démonstration (ensembliste)

(P. LOUQUET, A. VOGT, Probabilités, Combinatoire, Statistiques, Armand Colin éd., 1971)

• Notons le nombre de combinaisons avec répétition de k éléments pris parmi n.

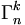
Chacune de ces combinaisons avec répétition s'écrit avec k éléments (répétés ou non). Si on les écrit in extenso, on utilisera donc k éléments. Les n éléments jouant un rôle symétrique, chacun apparaîtra donc fois. Soit x l'un de ces éléments (apparaissant donc fois). (1) Calculons d'une autre manière le nombre de fois où il apparaît.

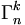
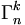
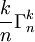
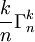
• Parmi les combinaisons avec répétition précédentes, le nombre de celles contenant x (une ou plusieurs fois) est : .

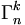
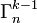
En effet, x étant imposé au moins une fois, on ne choisit plus que (k - 1) éléments, distincts ou non, sans ordre, mais toujours parmi n (car rien n'empêche que x soit répété et donc puisse réapparaître).

Chacune de ces combinaisons avec répétition contenant au moins une fois x, cela nous assure d'ores et déjà apparitions de x. (2)

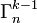
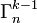
• Enlevons à présent une fois x de chacune de ces combinaisons.

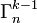
Chacune d'entre elles ne contient plus à présent que (k - 1) éléments (répétés ou non), il nous reste donc en tout éléments. Nous n'avons plus d'hypothèse sur les (k - 1) éléments restants dans chaque combinaison avec répétition, chacun des n éléments joue donc un rôle symétrique et apparaît donc fois (en particulier x) (3).

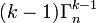
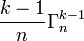
• Confrontons nos deux méthodes de calcul : nous avons donc : (1) = (2) + (3)

Soit : = + = Ce qui nous donne finalement : = .

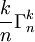
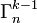
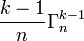
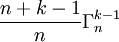
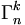
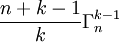
• Par récurrence, on obtient donc, de proche en proche :

= = = ... Soit finalement : =

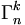
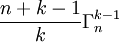
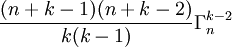
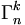
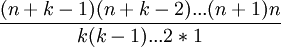
• On peut aussi écrire : =

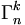
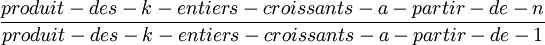
Ou encore, avec les factorielles : Ou enfin, avec les coefficients binomiaux :

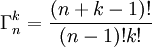
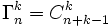
Algorithme efficace de génération des Combinaisons avec répétition

Le plus efficace, et le plus simple, pour calculer le nombre de combinaisons avec répétitions est encore d'utiliser l'algorithme calculant le nombre de combinaisons sans répétitions, comme décrit sur la page Combinaison. En effet, comme indiqué plus haut le nombre de combinaisons de "k" objets parmi "n" avec répétitions est le même que le nombre de combinaisons de "k" objets parmi "n+k-1" sans répétitions. En Ocaml et avec des entiers sur 64 bits, l'implémentation est la suivante :

      open Int64;;                                          (* Chargement du module de calcul arithmétique sur 64 bits (marche aussi sur machines 32 bits) *)      let kcombinaison (n : int64) (k : int64) : int64 =    (* Deux arguments, n et k, de type entiers signés sur 64 bits                                  *)         let n = sub (add n k) 1L in                        (* n devient n+k-1. Toute la suite correspond au calcul du nb de combinaisons sans répétitions *)         let nk = sub n k in                                (* Calcul de nk = n - k pour éviter de le refaire trop souvent                                 *)         let (k,nk) = if k<nk then (k,nk) else (nk,k)       (* Ce calcul est symétrique selon k ou nk, donc on calcule pour le plus facile/petit des deux  *)         let i = ref 1L and r = ref 1L in                   (* Initialisation de notre compteur "i", et de "r" pour stoquer le résultat intermédiaire      *)         while !i <= k do            r := div (mul !r (add nk !i)) !i;               (* Les propriétés du nb de combinaisons garantissent que toutes ces divisions sont sans reste  *)            i := succ !i;         done; !r                                           (* Il ne reste plus qu'à rendre le résultat final                                              *)      ;;      

Ceci permet de calculer par exemple le nombre de k-combinaisons de 20 parmi 40, qui ne peut pas être représenté en 32 bits ni calculé par l'algorithme itératif:

      # kcombinaison 40L 20L;;      - : int64 = 2794563003870330L