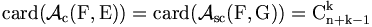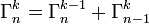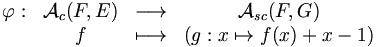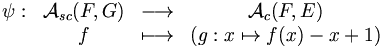Combinaison avec répétition - Définition

Première approche

En mathématiques, lorsque nous choisissons k objets parmi n objets discernables, chaque objet pouvant être répété (au plus k fois), nous obtenons un groupement non ordonné de k objets éventuellement répétés. Mais ce n’est pas acceptable en mathématiques de définir une k-combinaison avec répétition de cette façon, puisqu'un tel groupement n'est pas un ensemble (en effet la définition en extension d'un ensemble empêche la répétition des éléments et par exemple {1, 1, 2, 2, 2, 3}={1, 2, 3})..

Définition :

Une k-combinaison avec répétition d'un ensemble fini E de cardinal n, est une application f de E dans {0, 1, ..., k}, telle que

.

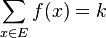
Plus précisément, si E={x₁, x₂, ..., x_n} alors f vérifie

.

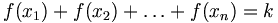
f s'appelle aussi une combinaison de n éléments pris k à k.

Remarque :

Cette application indique pour chaque élément de E le nombre de fois qu'il est choisi; et si l'application associe la valeur 0 à un élément de E, alors l'élément n'est pas choisi. De plus la somme des nombres de répétitions doit bien être égale à k, si nous voulons exactement k objets éventuellement répétés.

Exemple :

Dans un jeu de dominos, un domino est une 2-combinaison avec répétition de l'ensemble E={blanc, 1, 2, 3, 4, 5, 6}. Chaque domino peut être représenté par une application de E dans {0, 1, 2} qui associe à chaque élément de E le nombre de fois où l'élément apparaît sur le domino.
Ainsi le domino blanc, est représenté par l'application f définie par

f(blanc)=2, f(1)=0, f(2)=0, f(3)=0, f(4)=0, f(5)=0 et f(6)=0

et le domino blanc, 1 par l'application f définie par

f(blanc)=1, f(1)=1, f(2)=0, f(3)=0, f(4)=0, f(5)=0 et f(6)=0

Nombre de combinaisons avec répétition

Théorème :

Soit E un ensemble fini de cardinal n ( ). Alors l'ensemble K_k(E) des k-combinaisons avec répétition de E est fini et son cardinal est égal à

,

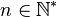
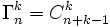
qui est le nombre de k-combinaisons de n+k-1 éléments.

se lit « Gamma nk ».

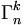
Démonstration :

Les combinaisons avec répétition sont des applications d'un ensemble fini dans un autre ensemble fini donc K_k(E) est fini. Supposons que E={x₁, x₂, ..., x_n}. L'ensemble K_k(E) se partitionne en l'ensemble K' des combinaisons qui envoient x₁ sur 0 (représentées par un k-uplet croissant dans lequel x₁ n'apparaît pas) et l'ensemble des combinaisons qui envoient x₁ sur un entier naturel non nul (représentées par un k-uplet croissant dans lequel x₁ apparaît au moins une fois). En restreignant une combinaison de K' à F=E\{x₁} (ce qui revient à la considérer comme un k-uplet croissant d'éléments de F), nous voyons qu'il y a autant d'éléments dans K' que de combinaisons avec répétition de n-1 éléments pris k à k donc . En retranchant 1 à la valeur en x₁ d'une combinaison de (ce qui revient à « éliminer un x₁ » du k-uplet correspondant pour obtenir un (k-1)-uplet), nous transformons cette combinaison en une combinaison avec répétition de n éléments pris k-1 à k-1. Réciproquement, en ajoutant 1 à la valeur en x₁ d'une combinaison de n éléments pris k-1 à k-1, nous obtenons un élément de .
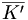
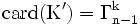
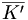
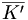
Il y a donc autant d'éléments dans que de combinaisons avec répétition de n éléments pris k-1 à k-1 donc .
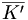
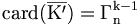
En écrivant

,

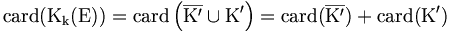
nous obtenons la formule de récurrence

De plus nous avons pour tout entier naturel n non nul, et pour tout entier naturel k et , et nous en déduisons le résultat.

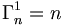
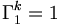
Autre démonstration :

Nous avons vu qu'il y avait une bijection entre l'ensemble des k-combinaisons avec répétition d'un ensemble E et l'ensemble des applications croissantes de F={1, 2, ..., k} dans E. Il suffit donc de déterminer le cardinal de ce dernier ensemble que nous noterons .

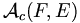
Théorème :

Soient n et k deux entiers naturels non nuls, E un ensemble totalement ordonné fini de cardinal n, et F={1, 2, ..., k}. Alors l'ensemble des applications croissantes de F dans E est fini et son cardinal est le nombre de k-combinaisons avec répétition de E, égal à . Et ce cardinal se note .

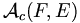
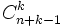
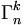
Démonstration :

Sans perte de généralité, nous pouvons supposer que E={1, 2, ..., n}. Nous allons transformer une application croissante de F dans E en une application strictement croissante de F dans une autre ensemble G, en lui ajoutant l'application x ↦ x – 1.
Posons G={1, 2, ..., n+k-1} et notons l'ensemble des applications strictement croissantes de F dans G. À une application croissante f de F dans E, associons l'application g de F dans G définie par

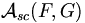
∀ x ∈ F, g(x)=f(x)+x-1

Il est facile de vérifier que l'application

est bien définie. Et l'application

est l'application réciproque de ϕ.

D'où .