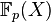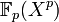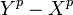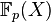Corps parfait - Définition

Exemples

Tout corps fini est parfait (cf le paragraphe propriétés).

Tout corps de caractéristique nulle est parfait. Un corps de caractéristique nulle est un corps où la somme réitérée de l'unité n'est jamais égale à zéro. Ainsi les corps des nombres rationnels et ses extensions ainsi que le corps des nombres réels est parfait (cf le paragraphe propriétés).

Cependant, tous les corps ne sont pas parfaits. Considérons le corps des fractions rationnelles sur le corps fini de cardinal p, où p est premier, et Ω sa clôture algébrique. Si K est choisi comme étant égal à l'ensemble des fractions de , alors K contient un polynôme non séparable. Considérons le polynôme P[X] de K[Y] égal à . Ce polynôme possède une unique racine X qui est donc un élément algébrique de degré p. De plus ce polynôme est irréductible. On en déduit que est le corps de décomposition du polynôme P[X]. Comme X est sa seule racine, P[X] n'est pas séparable.