Corps parfait - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définition - Propriétés - Exemples

Introduction

En mathématiques et plus particulièrement en algèbre dans le contexte de la théorie de Galois, un corps parfait est un corps dont toutes les extensions algébriques sont séparables.

Les corps parfaits sont utiles pour la théorie de Galois, car les théorèmes fondateurs, comme le théorème de l'élément primitif ou le théorème fondamental de la théorie de Galois utilisent dans les hypothèses le fait que l'extension considérée est séparable.

Les corps parfaits sont relativement fréquents, en effet, tout corps de caractéristique nulle comme ceux des nombres rationnels, des nombres réels ou des nombres complexes sont parfaits. C'est aussi le cas des corps finis.

Définition

Soit K un corps et L une extension algébrique de K.

Un corps K est dit parfait si et seulement si toutes ses extensions algébriques sont séparables.

Dire qu'une extension est séparable signifie que tout polynôme minimal d'un élément de L à coefficient dans K n'admet aucune racine multiple dans sa clôture algébrique.

Propriétés

Critère de séparabilité

Article détaillé : Extension séparable

L'analyse des extensions séparables permet d'établir critères de séparabilité d'un polynôme.

Un polynôme est séparable si et seulement si lui et sa dérivée formelle sont premiers entre eux.

Dans le cas d'un polynôme irréductible, car particulièrement intéressant dans le cadre de la théorie de Galois, cette proposition implique le corollaire suivant :

Un polynôme irreductible est séparable si et seulement si sa dérivée formelle n'est pas nulle.

Supposons K de caractéristique p et P[X] un polynôme irreductible. Il est séparable si et seulement s'il n'existe pas de polynôme Q[X] dans K[X] tel que l'on ait l'égalité P[X]=Q[X^p].

Ces propositions sont démontrées dans l'article détaillé.

Soit L une extension de K et M une extension de L. Alors si M est séparable sur K si et seuelement si M est séparable sur L et L est séparable sur K.

Soit m un élément de M et M_L[X] son polynôme minimal sur L. M_L[X] divise le polynôme minimal M_K[X]de m sur K. Soit Q[X] le polynôme de L[X] qui vérifie l'égalité M_K[X] = M_L[X] . Q[X]. Cette égalité montre que si M_K[X] n'admet pas de racine multiple, alors M_L[X] n'en admet pas non plus. Le fait que L soit séparable sur K est une évidence car L est contenu dans M.

Caractérisation des corps parfaits

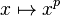
Théorème — Un corps $K$ est parfait si et seulement s'il est de caractéristique nulle, ou, lorsqu'il est de caractéristique $p > 0$ , l'homomorphisme de Frobenius $x\mapsto x^{p}$ est surjectif (autrement dit tout élément de K possède une racine p-ième dans $K$ ). En particulier tout corps fini est parfait.

Si un corps est de caractéristique nulle, alors il est parfait.

Soit P[X] le polynôme minimal de l un élément de L. Soit n son degré, alors le terme de degré n-1 de sa dérivée est égal à nX^n-1. Ce terme n'est nulle que si la caractéristique du corps est égal à n. Si le corps est de caractéristique nulle, alors la dérivée formelle n'est pas nulle et le polynôme minimal n'admet pas de racine multiple.