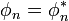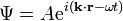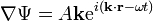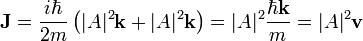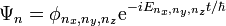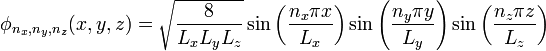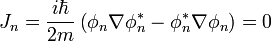Courant de probabilité - Définition

Exemples

Particule libre

L'amplitude de probabilité d'une particule libre est une onde plane tridimensionnelle représentée par :

avec le vecteur d'onde, le vecteur position et ω la fréquence angulaire.

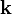
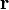
le gradient de la fonction est donné par :

on obtient le gradient de la fonction complexe conjuguée de manière similaire et finalement :

avec la vitesse de la particule. On a utilisé la relation avec l'impulsion de la particule.

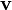
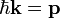
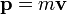
Remarquons que le courant de probabilité n'est pas nul même si la densité de probabilité | Ψ | ² = | A | ² est indépendante du temps.

Particule dans une boîte

Les états stationnaires d'une particule dans une boîte de dimension L_x,L_y,L_z ont une fonction d'amplitude définie par :

avec

et on a :

puisque .