Densité de probabilité - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Densité de probabilité d'une variable aléatoire réelle - Fonction de variables aléatoires à densité - Densité de probabilité d'un vecteur aléatoire

Introduction

En théorie des probabilités ou en statistiques, une densité de probabilité est une fonction qui permet de représenter une loi de probabilité sous forme d'intégrales.

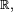
Formellement, une loi de probabilité possède une densité ƒ, si ƒ est une fonction définie sur $\ \scriptstyle\mathbb{R},\$ positive ou nulle et Lebesgue-intégrable, telle que la probabilité de l'intervalle [a, b] est donnée par

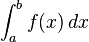
pour tous nombres a. Par exemple, si la variable X a pour densité de probabilité la fonction ƒ, la probabilité que la variable X soit dans l'intervalle [4,3, 7,8] sera

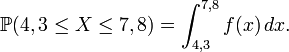
$\mathbb{P}(4,3 \leq X \leq 7,8) = \int_{4,3}^{7,8} f(x)\,dx.$
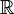
Cela implique que l'intégrale de ƒ sur tout $\ \mathbb{R}\$ donne 1. Réciproquement, pour toute fonction ƒ positive ou nulle et Lebesgue-intégrable, d'intégrale égale à 1 :
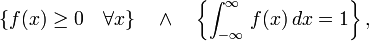
$\left\{f(x) \geq 0\quad \forall x\right\}\quad \and\quad\left\{ \int_{-\infty}^\infty \,f(x)\,dx = 1\right\},$
il existe une loi de probabilité ayant ƒ pour densité de probabilité.

Intuitivement, si une loi de probabilité a pour densité ƒ, alors l'intervalle infinitésimal [x, x + dx] a pour probabilité ƒ(x) dx.

Informellement, une densité de probabilité peut être vue comme la limite d'un histogramme : si on dispose d'un échantillon suffisamment important de valeurs d'une variable aléatoire à densité, représenté par un histogramme des fréquences relatives des différentes classes de valeurs, alors cet histogramme va ressembler à la densité de probabilité de la variable aléatoire, pourvu que les classes de valeurs soient suffisamment étroites.
Densité de probabilité d'une variable aléatoire réelle

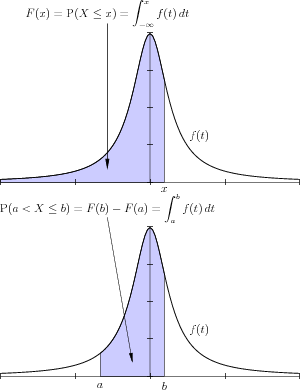
Lien entre la densité, f et la fonction de répartition (haut), et, plus généralement, les probabilités (bas).

Définition — En théorie des probabilités ou en statistiques, on dit qu'une fonction $\scriptstyle\ f\$ est une densité de probabilité d'une variable aléatoire réelle $\scriptstyle\ X\$ si, pour tout réel $\scriptstyle\ x,$
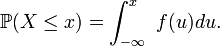
$\mathbb{P}(X\le x)= \int_{-\infty}^{x}\ f(u)du.$

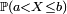
La probabilité $\scriptstyle\ \mathbb{P}(a < X \le b)\$ se calcule alors par la relation suivante :
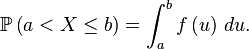
$\mathbb{P}\left( a < X \le b \right)=\int_a^b f\left( u \right)\,du.$
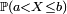
En traçant la représentation graphique de la densité de probabilité, la probabilité $\scriptstyle\ \mathbb{P}(a < X \le b)\$ se lit comme l'aire sous la courbe sur l'intervalle $\scriptstyle\ [a , b].$

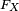
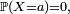
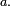
En conséquence, la fonction de répartition $\scriptstyle\ F_X\$ de $\scriptstyle\ X\$ est continue, et $\scriptstyle\ \mathbb{P}(X=a) = 0,$ pour tout nombre réel $\scriptstyle\ a.$ En cela, le comportement d'une variable à densité est très différent de celui d'une variable discrète.

Définition informelle de la densité de probabilité

La définition qui suit est une reformulation de la définition intégrale proposée en début d'article. C'est la définition utilisée en général par les physiciens, en particulier ceux issus du domaine de la physique statistique.

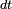
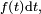
Si $\scriptstyle\ dt\$ est un nombre réel positif infiniment petit, alors la probabilité que $\scriptstyle\ X\$ soit inclus dans l'intervalle $\scriptstyle\ [t,t+dt]\$ est égale à $\scriptstyle\ f\left(t\right)\mathrm dt,$ soit:
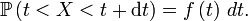
$\mathbb{P}\left(t < X < t+ \mathrm dt \right)= f\left(t\right)\, dt.$
Cette « définition » est très utile pour comprendre intuitivement à quoi correspond une densité de probabilité, et est correcte dans beaucoup de cas importants. On peut tracer une analogie avec la notion de densité de masse, ou encore avec la notion de densité de population. Une formulation plus mathématique serait
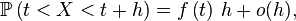
$\mathbb{P}\left(t < X < t+ h \right)= f\left(t\right)\,h+o(h),$
ce qui permet de comprendre en quoi la définition donnée en physique n'est pas complètement rigoureuse :
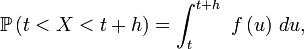
$\mathbb{P}\left(t < X < t+ h \right)= \int_t^{t+h}\ f\left(u\right)\,du,$
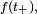
et il est alors facile de vérifier que si $\scriptstyle\ f\$ possède une limite à droite en $\scriptstyle\ t\$ , notons-là $\scriptstyle\ f(t_+),$ on a alors
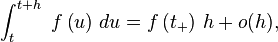
$\int_t^{t+h}\ f\left(u\right)\,du = f\left(t_+\right)\,h+o(h),$
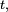
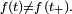
ce qui corrobore la définition physique lorsque $\scriptstyle\ f\$ est continue à droite en $\scriptstyle\ t,$ mais la met en défaut quand $\scriptstyle\ f(t)\neq f(t_+).$ Bien sûr, les densités de probabilités usuelles sont continues à droite sauf éventuellement en un nombre fini (et en un petit nombre) de points.

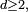
Notons que ce genre d'interprétation infinitésimale (ou issue de la physique) s'étend aux dimensions $\scriptstyle\ d\ge 2,$ voir la section suivante.

Densité de la médiane de 9 variables i.i.d. :

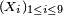
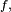
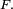
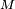
Soit $\scriptstyle\ (X_i)_{1\le i\le 9}\$ une suite de 9 v.a. r. i.i.d. de même densité $\scriptstyle\ f,$ et de même fonction de répartition $\scriptstyle\ F.$ Notons $\scriptstyle\ M\$ la médiane de cette suite. Alors :
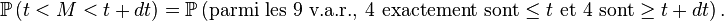
$\mathbb{P}\left(t < M < t+ dt \right)=\mathbb{P}\left(\text{parmi les 9 v.a.r., 4 exactement sont}\le t\text{ et 4 sont}\ge t+dt\right).$
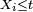
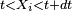
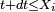
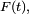
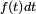
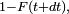
On peut voir cela comme une suite de 9 expériences aléatoires indépendantes faites dans les mêmes conditions, avec à chaque fois 3 issues : " $\scriptstyle\ X_i\le t\$ ", " $\scriptstyle\ t<X_i<t+dt\$ " et " $\scriptstyle\ t+dt\le X_i\$ ", de probabilités respectives $\scriptstyle\ F(t),$ $\scriptstyle\ f(t)dt\$ et $\scriptstyle\ 1-F(t+dt),$ donc la probabilité ci dessus est donnée par la loi multinomiale de paramètres 3, 9 et $\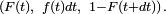scriptstyle\ \left(F(t),\ f(t)dt,\ 1-F(t+dt)\right).$ Ainsi :
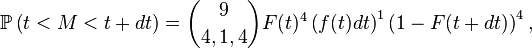
$\mathbb{P}\left(t < M < t+ dt \right)={9\choose 4,1,4}F(t)^4\left(f(t)dt\right)^1\left(1-F(t+dt)\right)^4,$
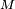
et la densité de $\scriptstyle\ M\$ est
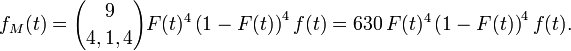
$f_M(t)={9\choose 4,1,4}F(t)^4\left(1-F(t)\right)^4f(t)=630\,F(t)^4\left(1-F(t)\right)^4f(t).$
Cette méthode est détaillée dans le livre de David. Un résultat plus général se trouve dans Statistique d'ordre.

Critères d'existence d'une densité

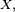
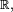
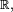
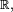
En vertu d'un théorème dû à Lebesgue, la fonction de répartition d'une variable aléatoire réelle $\scriptstyle\ X,$ étant croissante, est dérivable presque partout sur $\scriptstyle\ \mathbb{R},\$ et la dérivée ainsi obtenue est positive et intégrable sur $\scriptstyle\ \mathbb{R},\$ d'intégrale inférieure ou égale à 1.

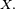
Critère 1 — $\scriptstyle\ X\$ possède une densité de probabilité si et seulement si l'intégrale, sur $\scriptstyle\ \mathbb{R},\$ de la dérivée de la fonction de répartition est exactement égale à 1. Cette dérivée est alors une des densités de probabilité de $\scriptstyle\ X.$

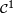
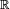
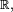
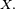
Critère 2 — Si la fonction de répartition de $\scriptstyle\ X\$ est de classe $\scriptstyle\ \mathcal{C}^1$ par morceaux sur $\scriptstyle\ \mathbb{R}$ et est, d'autre part, continue sur $\scriptstyle\ \mathbb{R},\$ alors la dérivée de la fonction de répartition de $\scriptstyle\ X\$ est une des densités de probabilité de $\scriptstyle\ X.$

Densité de la médiane de 9 variables i.i.d. (bis) :

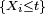
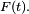
Pour le calcul de la densité de la médiane de 9 variables i.i.d., une solution plus rigoureuse que celle de la section précédente, mais plus lourde, est de calculer la fonction de répartition de la médiane, puis de la dériver. On reconnait un schéma de Bernoulli : le nombre d'indices $\scriptstyle\ i\$ tels que $\scriptstyle\ \{X_i\le t\}\$ suit une loi binomiale de paramètres 9 et $\scriptstyle\ F(t).$
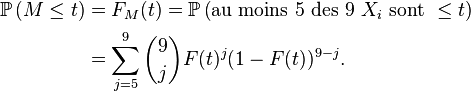
$\begin{align} \mathbb{P}\left(M\le t\right) &= F_{M}(t) = \mathbb{P}\left(\text{au moins 5 des 9 }X_i\text{ sont }\le t\right) \\ &=\sum_{j=5}^9{9 \choose j}F(t)^j(1-F(t))^{9-j}. \end{align}$
En dérivant, on trouve :
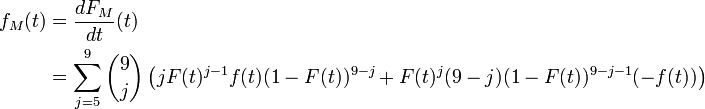
$\begin{align} f_{M}(t) & {} ={dF_{M} \over dt}(t)\\ & {} =\sum_{j=5}^9{9 \choose j}\left(jF(t)^{j-1}f(t)(1-F(t))^{9-j} +F(t)^j (9-j)(1-F(t))^{9-j-1}(-f(t))\right) \end{align}$
Après quelques manipulations sur les coefficients binomiaux, tous les termes de cette somme se télescopent, sauf une partie du premier terme, ce qui donne :
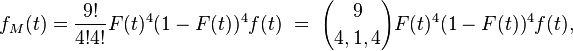
$f_{M}(t) = {9! \over 4!4!} F(t)^{4} (1-F(t))^{4} f(t)\ =\ {9 \choose 4,1,4}F(t)^{4} (1-F(t))^{4} f(t),$
puis
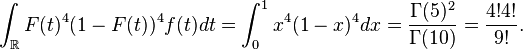
$\int_{\mathbb R}F(t)^{4} (1-F(t))^{4} f(t)dt = \int_{0}^1 x^{4} (1-x)^{4}dx = \frac{\Gamma(5)^2}{\Gamma(10)} = \frac{4!4!}{9!}.$
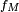
Pour les deux dernières égalités, se référer aux pages sur la fonction bêta et sur la fonction gamma. Il en découle que $\scriptstyle\ f_M\$ satisfait le critère 1. CQFD

On pourra consulter le livre de David (pages 8-13) pour plus de détails.

Fonction de variables aléatoires à densité
- Introduction - Densité de probabilité d'une variable aléatoire réelle - Fonction de variables aléatoires à densité - Densité de probabilité d'un vecteur aléatoire

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

1
Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Existe-t-il des mélodies naturelles ? 🎶

Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

1
Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Le trou noir supermassif Ansky vient de se réveiller ⚫

1
Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

Page générée en 0.123 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise