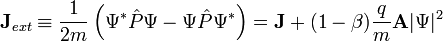Courant de probabilité - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mécanique quantique, le courant de probabilité est un concept décrivant le flux de densité de probabilité. Tout comme la loi de conservation de la charge en électrodynamique, il existe une loi de conservation de la densité de probabilité en mécanique quantique. Intuitivement, cette dernière indique que lorsque la densité de probabilité dans volume fixé varie dans le temps, alors il doit exister un flux de densité de probabilité à travers les parois de ce volume. La notion de courant de probabilité permet de décrire ce flux de probabilité.
Définition
Ainsi qu'on l'a déjà mentionné, la densité de probabilité satisfait une condition de conservation locale. En notant
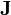
avec Ψ la fonction d'onde représentant l'amplitude de probabilité et, par définition, | Ψ | 2 = Ψ * Ψ, la densité de probabilité. Cette condition est satisfaite si l'on définit
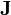
Du théorème de la divergence, on a (en partant de l'équation de continuité) que :
avec
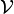
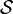
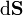
Explicitement cette dernière relation signifie que le courant de probabilité passant à travers une surface (fermée) est égal à la diminution en probabilité de trouver la particule dans le volume borné par cette surface.
Etat stationnaire
Supposons que le potentiel V du système soit indépendant du temps, il existe alors un ensemble complet d'états (vecteurs propres de l'Hamiltonien) ayant la forme suivante :
où la fonction φn satisfait l'équation de Schrödinger indépendante du temps :
Pour n'importe quel état stationnaire, la densité de probabilité est stationnaire, en effet,
et comme φn est indépendante du temps,
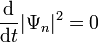
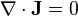
ce qui signifie que le flux total de densité de probabilité à travers n'importe quelle surface fermée est nul. Par ailleurs, l'expression du courant de probabilité pour l'état n se simplifie :
Démonstration de l'équation de continuité
On suppose que Ψ est la fonction d'onde correspondant à l'amplitude de probabilité d'une particule (dans l'espace des positions). La probabilité de trouver la particule dans un certain volume
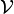
en prenant la dérivée temporelle de cette probabilité et en utilisant la règle de Leibniz pour la dérivée d'une intégrales paramétriques, on a :
L'équation de Schrödinger donne :
avec m la masse de la particule,
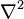
En prenant le complexe conjugué, on a aussi :
et en utilisant ces deux dernières équations, on a
Cependant, on peut réécrire
en effet la règle du produit donne :
et le deuxième et le dernier terme se simplifient. Finalement, en définissant
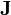
on a :
et donc :
Définition dans un champ extérieur
La définition doit être modifiée pour un système dans un champ électromagnétique extérieur. Par exemple, pour une particule de charge q, l'équation de Schrödinger indépendante du temps qui satisfait une invariance locale de jauge est donnée dans l'espace des positions avec un Hamiltonien de couplage minimal par :
avec
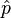
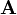
Si on remplace
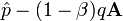
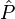
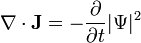
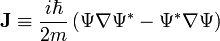
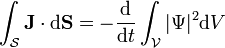
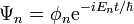
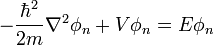
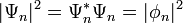
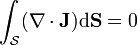
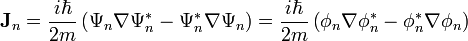
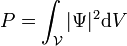
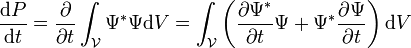
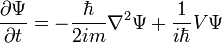
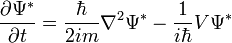
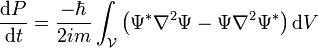
![\Psi^*\nabla^2\Psi-\Psi\nabla^2\Psi^* = \nabla\cdot \left[\Psi^*\nabla\Psi -\Psi\nabla \Psi^*\right]](https://static.techno-science.net/illustration/Definitions/autres/e/e0a8d6ca95a28b6ec3f25d098426996b_a8c74fe66f749199413cf7ea0a681c59.png)
![\nabla\cdot \left[\Psi^*\nabla\Psi -\Psi\nabla \Psi^*\right] = \Psi^*\nabla^2\Psi+\nabla\Psi^*\cdot\nabla\Psi-\Psi\nabla^2\Psi^*-\nabla\Psi\cdot\nabla\Psi^*](https://static.techno-science.net/illustration/Definitions/autres/8/8c60b087ba18c5bbb250018ea41a923a_ae86c972fb1b47d0fc3f3ca741239439.png)
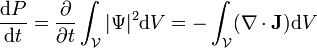
![\hat{H} = {1\over 2m}\left[\hat{p}-(1-\beta)q \mathbf{A}(t)\right]^2- \beta q \mathbf F(t) \cdot \mathbf r](https://static.techno-science.net/illustration/Definitions/autres/3/30ed3289146938c27ac4984f56e4dece_8a28e7951be780c9dad7ff5ca7815159.png)