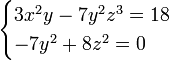Dixième problème de Hilbert - Définition
La liste des auteurs de cet article est disponible ici.
Réponse au dixième théorème de Hilbert
Un exemple de système d'équations diophantiennes est le suivant :
La question qui se pose s'énonce ainsi: existe-t-il des nombres entiers x, y et z qui satisfont simultanément les deux équations? Cette question est équivalente à celle de savoir si une équation diophantienne unique à plusieurs variables admet une solution dans les entiers naturels. Par exemple, le système ci-dessus a une solution entière si et seulement si l'équation suivante a une solution dans les entiers naturels :
- (3(x1 − x2)2(y1 − y2) − 7(y1 − y2)2(z1 − z2)3 − 18)2 + ( − 7(y1 − y2)2 + 8(z1 − z2)2)2 = 0
Youri Matiiassevitch a utilisé une astuce impliquant les nombres de Fibonacci afin d'exhiber une équation diophantienne dont les solutions se développent exponentiellement. Les premiers travaux sur ce sujet sont dus à Julia Robinson, Martin Davis et Hilary Putnam; ils avaient démontré qu'il suffit de ce résultat pour qu'il n'existe aucun algorithme général décidant l'existence de solutions pour les équations diophantiennes.
Des travaux postérieurs ont montré que la question de l'existence de solutions d'une équation diophantienne est indécidable même si l'équation a seulement 9 variables naturelles (Matiyasevich, 1977) ou 11 variables entières (Zhi Wei Sun, 1992).