Extremum - Définition

Introduction

L'expression « élément extremum » signifie « élément maximum » ou « élément minimum ».

Dans un ensemble ordonné E, un élément d'une partie A est le plus grand élément ou maximum de A, s'il appartient à A et est supérieur à tout autre élément de A. L'existence d'un maximum n'est en général pas assurée pour toute partie d'un ensemble ordonné. En revanche, sous condition d'existence, un tel élément est unique (ce qui justifie l'emploi de l'article défini « le » dans la définition). De manière analogue, le plus petit élément ou minimum est, s'il existe, un élément de A inférieur à tout autre élément de A.

Généralités

Unicité

Si une partie A de E admet deux maxima, m₁ et m₂, alors m₁ est plus grand que tout élément de A, donc en particulier que m₂ ; et de même, m₂ est plus grand que m₁. Par antisymétrie des relations d'ordre, l'égalité m₁=m₂ s'en déduit.

Comparaison avec d'autres notions

D'autres notions relatives aux ensembles ordonnés sont proches de celles de maximum ; les comparer permet de mieux les appréhender :

• La notion de majorant : un élément de E est un majorant de A s'il est plus grand que tout élément de A. Ainsi, un maximum est en particulier un majorant ;
• La notion de borne supérieure : un élément est une borne supérieure de A si c'est le plus petit de tous les majorants de A (une borne supérieure de A est donc définie comme le minimum d'une certaine partie). Si A admet un maximum, alors ce maximum est la borne supérieure de A ;
• La notion d'élément maximal : un élément de A est maximal dans A, s'il appartient à A, et n'est inférieur à aucun autre élément de A. Un maximum est toujours un élément maximal, et les deux notions coïncident dans les ensembles munis d'un ordre total.

Exemples

L'ensemble N des entiers naturels muni de son ordre usuel admet un plus petit élément, à savoir 0. Il n'admet en revanche pas de plus grand élément. Une propriété assure toutefois que toute partie majorée de N (c'est-à-dire admettant un majorant), admet un maximum.

Dans l'ensemble R des nombres réels muni de son ordre usuel, certaines parties majorées n'admettent pas de plus grand élément, par exemple l'intervalle ]0,1[ des nombres strictement compris entre 0 et 1.

Dans un ensemble ordonné muni d'un ordre non total, certaines parties admettent des éléments maximaux qui ne sont pas des maxima. Par exemple dans l'ensemble des parties de l'ensemble {0,1}, ordonné par l'inclusion, la partie A = {{0},{1}} amdet deux éléments maximaux, mais pas de maximum.

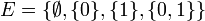
Autre exemple

• Prenons pour ensemble ordonné E l'ensemble des intervalles réels, ordonné par la relation d'inclusion.
• Choisissons comme partie P à étudier, l'ensemble des intervalles inclus dans .
• Tout élément de P inclut l'ensemble vide, donc l'ensemble vide est un minorant de P. Or l'ensemble vide est élément de P, c'est donc aussi sa borne inférieure et son plus petit élément.
• Tout élément de P est inclus dans l'intervalle [-1 ; 1] qui est élément de E mais pas de P. Donc [-1 ; 1] est un majorant de P, mais pas son plus grand élément. Malgré tout, c'est son plus petit majorant, donc sa borne supérieure.
• Il n'existe aucun élément de P qui soit supérieur à ]0 ; 1]. ]0 ; 1] est donc un élément maximal de P. Mais il existe des éléments de P qui ne lui sont pas comparables, par exemple [1/2 ; 3/2]. Donc ]0 ; 1] n'est pas le plus grand élément de P. Et pour cause, il existe un autre élément maximal distinct : [-1 ; 0[, donc P n'a pas de plus grand élément !