Extremum - Définition
La liste des auteurs de cet article est disponible ici.
Fonction optimum de deux fonctions
Les fonctions minimum et maximum de deux fonctions peuvent être définies à l'aides de valeurs absolues :
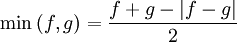
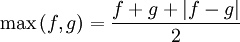
Extrema d'une fonction
Le maximum d'une fonction f définie sur un ensemble E et à valeurs dans un ensemble F ordonné est le maximum de l'ensemble des valeurs prises par f (de la partie f(E) de F). Ainsi m est le maximum de f s'il existe un élément a de E tel que f(a) = m et tel que pour tout élément x de E, f(x) ≤ f(a) ; l'élément a (qui n'est pas nécessairement unique) est appelé point de maximum de f.
Dans le cas où l'espace de départ de f est muni d'une structure topologique (par exemple si f est une fonction d'une ou plusieurs variables réelles à valeurs réelles), on distingue deux types d'extrema : les extrema globaux, qui correspondent à la définition précédente, et les extrema locaux.
Extremum local d'une fonction
Soient une fonction f définie sur un espace topologique E et a un point de E. On dit que f atteint en a un maximum local s'il existe un voisinage V de a tel que pour tout élément x de V, on ait f(x) ≤ f(a).
On dit alors que f(a) est un « maximum local » de f sur E et que a est un point de maximum local de f.
Théorèmes topologiques d'existence d'extremas globaux
Soit une fonction
L'existence d'extrema globaux est assurée dès lors que la fonction f est continue et définie sur une partie D compacte : en effet, l'image f(D) par une telle fonction continue d'une partie compacte est une partie compacte de l'espace d'arrivée R ; en tant que partie bornée de R, elle admet une borne supérieure, et cette borne supérieure est dans f(D) puisque cette partie est fermée.
En dimension k=1, c'est en particulier le cas si I est un intervalle fermé borné, c'est-à-dire de la forme [a,b] (voir théorème des bornes). En dimension supérieure k, c'est en particulier le cas si D est une boule fermée (de la forme
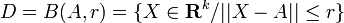
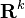
Méthodes issues du calcul différentiel pour la recherche d'extrema locaux.
Soit une fonction
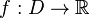
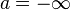
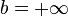
Si la fonction f atteint un extremum local en un point a où elle est différentiable, alors toutes ses dérivées partielles s'annulent en a ; en particulier, dans le cas d'une fonction d'une seule variable, le nombre dérivé de f en a est nul.
Pour cette raison, l'étude des extrema passe souvent par la recherche des points d'annulation de la dérivée, appelés points critiques de f. Un point critique n'est pas nécessairement un point d'extremum, comme le montre l'exemple de la fonction
-
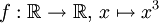
Cas d'une fonction d'une variable
- Condition suffisante pour un extremum local :
- Si f est dérivable sur I, et si a est un point intérieur à I où la dérivée de f s'annule en changeant de signe, alors f atteint un extremum local en a. Plus précisément, en supposant
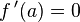
- S'il existe α réel strictement positif tel que
![[a-\alpha,\, a + \alpha] \subset I](https://static.techno-science.net/illustration/Definitions/autres/e/e651416c3f9e32be2dbb726e139ac207_588312f7495726baa073b98d29ec0342.png)
- et
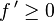
![[a-\alpha,\, a]](https://static.techno-science.net/illustration/Definitions/autres/9/90b20f5f95833dbdd9f2cf09e194d37e_b548495829b47d7f0693bb0827980a72.png)
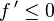
![[a,\, a + \alpha]](https://static.techno-science.net/illustration/Definitions/autres/7/7d2fb273c68d8938e6a1f00353232942_feddd1196a31ac1fbd08a8fc1c09404c.png)
- alors f atteint un maximum local en a.
- S'il existe α réel strictement positif tel que
![[a-\alpha,\, a + \alpha] \subset I](https://static.techno-science.net/illustration/Definitions/autres/e/e651416c3f9e32be2dbb726e139ac207_588312f7495726baa073b98d29ec0342.png)
- et
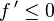
![[a-\alpha,\, a]](https://static.techno-science.net/illustration/Definitions/autres/9/90b20f5f95833dbdd9f2cf09e194d37e_b548495829b47d7f0693bb0827980a72.png)
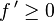
![[a,\, a + \alpha]](https://static.techno-science.net/illustration/Definitions/autres/7/7d2fb273c68d8938e6a1f00353232942_feddd1196a31ac1fbd08a8fc1c09404c.png)
- alors f atteint un minimum local en a.
- S'il existe α réel strictement positif tel que
- Remarque
La condition nécessaire pour un extremum local ne s'applique pas aux bornes de l'intervalle. Par exemple, la fonction
admet deux extremums globaux (a fortiori locaux), atteints en 0 et 1. Par ailleurs, elle est dérivable et sa dérivée ne s'annule en aucun point.
Cas des fonctions de plusieurs variables
Condition suffisante pour un extremum local :
- On suppose ici que A est un ouvert, et que f est de classe C2 sur A.
- On considère un point a de A. La (matrice) hessienne de f en a est notée
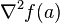
- Si
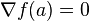
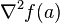
- Si
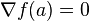
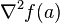
- Si
- Rappel : par définition, la hessienne de f en a est la matrice carrée d'ordre n ayant
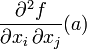
- Comme f est de classe C2, il résulte du théorème de Schwarz sur les dérivées partielles d'ordre 2 que la hessienne est symétrique.




![f : [0, 1] \to\R,\, x \mapsto x](https://static.techno-science.net/illustration/Definitions/autres/2/2d14b4188b88ac9a63a7f7025ba45bec_593c6d53da0bb15d5e572a003d220762.png)

















































