Formule de MacCullagh - Définition

Facteur de forme géodynamique

D'autre part, toujours dans l'hypothèse d'une symétrie axiale, le développement genéral du potentiel gravifique en multipôles limité aux termes d'ordre 2 s'écrit

où

,

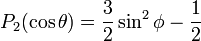
est le polynôme de Legendre de degré 2. On a donc

.

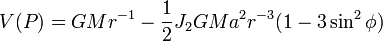
Dans le cas de la Terre, le coefficient géopotentiel zonal de degré 2, à savoir J₂, est souvent appelé « facteur de forme géodynamique ». On l'obtient par identification de cette dernière formule avec celle de MacCullagh, soit

.

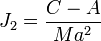
Certains géodésiens appellent aussi cette dernière relation « formule de MacCullagh », mais cet usage ne semble pas très judicieux.