Polynôme de Legendre - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les polynômes de Legendre sont des solutions de l'équation différentielle de Legendre, et constituent l'exemple le plus simple d'une suite de polynômes orthogonaux.
Équation de Legendre
On appelle équation de Legendre l'équation :
![\frac{\textrm{d}}{\textrm{d}x}[(1-x^{2})\frac{\textrm{d}y}{\textrm{d}x}]+n(n+1)y=0](https://static.techno-science.net/illustration/Definitions/autres/1/12a0ea83afb427dc0e005705e6f0df57_33776c7777cbd6a11597fea0816cd925.png)
On définit ainsi le polynôme de Legendre Pn (pour tout entier naturel n) :
![\frac{\textrm{d}}{\textrm{d}x}[(1-x^{2})\frac{\textrm{d}P_n(x)}{\textrm{d}x}]+n(n+1)P_n(x)=0,\qquad P_n(1)=1.](https://static.techno-science.net/illustration/Definitions/autres/e/e68fbe96c7f8a1126c73de004053f7bb_f3f8524d07b8574464fc287a2def5534.png)
On a donc
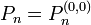
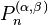
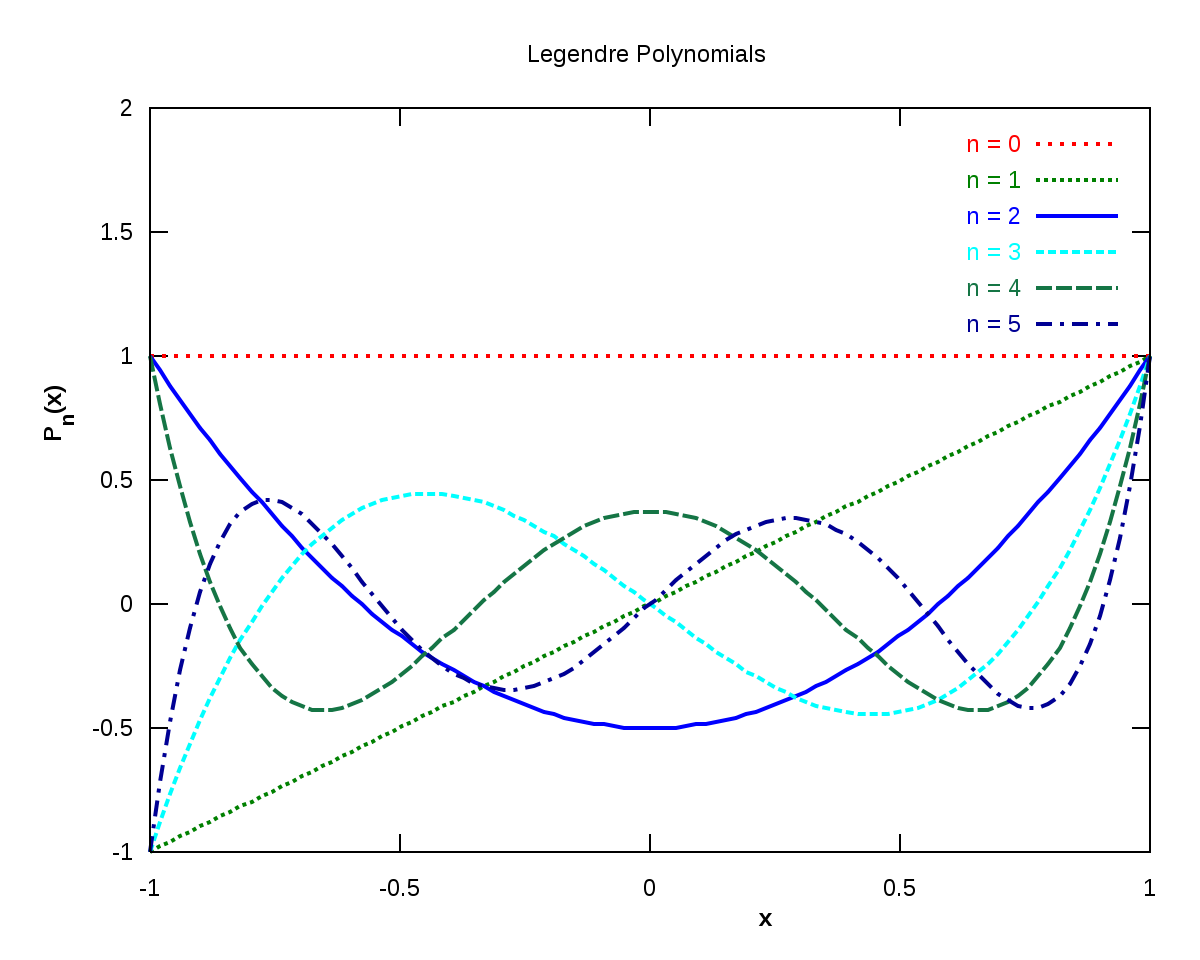
Quelques polynômes
Les premiers polynômes sont :

Autres définitions
Formule de récurrence de Bonnet
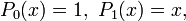
Formule de Rodrigues
On définit le polynôme Pn (pour tout entier naturel n) par :
Définition analytique
On peut aussi définir cette suite de polynômes par sa fonction génératrice :
Le théorème des résidus donne alors :
où le contour entoure l'origine et est pris dans le sens trigonométrique.
Définitions sous forme de somme
On définit ce polynôme de deux façons sous forme de somme :
(on en déduit
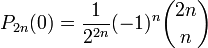
Décomposition en série de polynômes de Legendre
Décomposition d'une fonction holomorphe
Toute fonction f, holomorphe à l'intérieur d'une ellipse de foyers -1 et +1, peut s'écrire sous la forme d'une série qui converge uniformement à l'intérieur de l'ellipse:
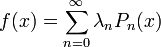
avec
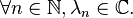
Décomposition d'une fonction lipschitzienne
On note
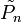
Soit f une application continue sur [-1,1]. Pour tout entier naturel n on pose
Alors la suite
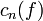
![\R_n[X]](https://static.techno-science.net/illustration/Definitions/autres/b/bbdf71fbc7163afedcc40f775beb1c24_0eebd04d43f5a83bfccdcd8915e43324.png)
On a de plus :
-
![\forall x\in[-1,1],\;S_nf(x)=\int\limits_{-1}^1 K_n(x,\;y)f(y)\,dy](https://static.techno-science.net/illustration/Definitions/autres/a/a101d8353b7a2c0007581d67dabc5b16_27d98bdbbf0ebce6401cfaff16e9b0f4.png)
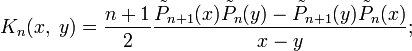
-
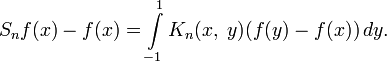
Supposons de plus que f est une fonction lipschitzienne. On a alors la propriété supplémentaire :[réf. souhaitée]
autrement dit, l'égalité
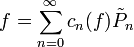
est vraie non seulement au sens L2 mais au sens de la convergence simple sur ]-1,1[.
Propriétés
Degré
Le polynôme Pn est de degré n.
Parité
Les polynômes de Legendre suivent la parité de n. On peut exprimer cette propriété par :
(en particulier, Pn( − 1) = ( − 1)n et P2n + 1(0) = 0).
Orthogonalité
Les polynômes orthogonaux les plus simples sont les polynômes de Legendre pour lesquels l'intervalle d'orthogonalité est [−1, 1] et la fonction poids est simplement la fonction constante de valeur 1 : ces polynômes sont orthogonaux par rapport au produit scalaire < , > défini sur
![\R[X]](https://static.techno-science.net/illustration/Definitions/autres/6/60ed190117e7614d227f8d1693161a5b_67a4b8800a94a9a175a1ac6f97f6cf7d.png)
 .
.
La définition même de Pn montre qu'il s'agit d'un vecteur propre pour la valeur propre -n(n+1) de l'endomorphisme:
Or cet endomorphisme est symétrique pour le produit scalaire précédent, puisqu'une intégration par parties montre que
- :
 .
.
Comme il s'agit de vecteurs propres associés à des valeurs propres distinctes, la famille des polynômes de Legendre est orthogonale.
Norme
Le carrré de la norme, dans L2([-1,1]), est
En effet, pour tout n>1, on peut établir la relation
dont on déduit (en utilisant que pour tout k, P'k − 1 est de degré k-2<k donc est orthogonal à Pk, et en effectuant une intégration par parties) :
Comme PnPn + 1 est impair et pour tout k, Pk(1) = 1, on aboutit ainsi à (2n + 1) | | Pn | | 2 = 2.
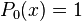
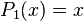
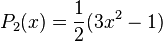
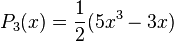
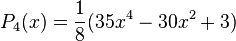
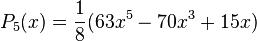
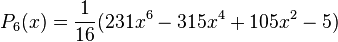
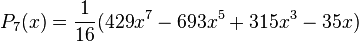
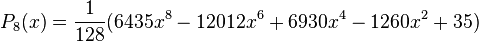
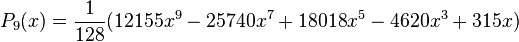
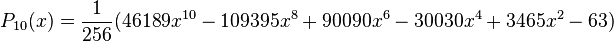
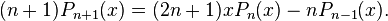
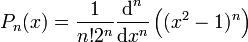
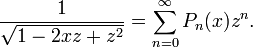
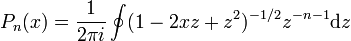
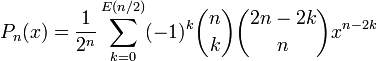
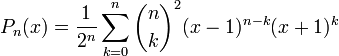
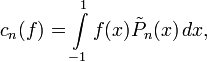
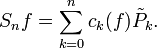
![\forall x\in]-1,1[,\;\lim_{n\to\infty}S_nf(x)=f(x).](https://static.techno-science.net/illustration/Definitions/autres/7/792a88feb9f2ba189034be8fbfdb195f_0fa367196e90cfcd6fd85ae8b9e921d2.png)
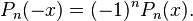
![P \in \R[X] \to u(P)= \frac{\textrm{d}}{\textrm{d}x}[(1-x^{2})\frac{\textrm{d}P}{\textrm{d}x}]](https://static.techno-science.net/illustration/Definitions/autres/f/f6369368f178d34a813764778268f1de_79899dacee69d854cc99bc2d9db220ee.png)
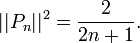
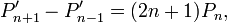
![<P_n,(2n+1)P_n>=<P_n,P'_{n+1}-P'_{n-1}>=<P_n,P'_{n+1}>=[P_nP_{n+1}]_{-1}^{\ 1}-<P'_n,P_{n+1}>=[P_nP_{n+1}]_{-1}^{\ 1}.](https://upload.wikimedia.org/math/4/2/6/426624b97534f713fd273a54bec16b8b.png)

















































