Groupe de Galois - Définition

Exemples

Cas d'un polynôme de degré deux

Considérons un premier exemple, suffisamment simple pour que l'approche historique soit utilisable dans ce cas. Soit P[X] le polynôme à coefficient rationnel défini de la manière suivante:

Si l'on note x₁ et x₂ les deux racines de P[X], alors:

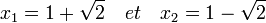
Considérons alors l'ensemble E des polynômes Q[X,Y] à deux variables tel que (x₁,x₂) soit racine. Les trois exemples de polynômes suivants vérifient cette propriété:

On remarque alors que (x₂,x₁) est aussi une racine d'un polynôme de cette nature. Ceci démontre que les deux permutations des racines, qui au couple (x₁,x₂) associent, l'une (x₁,x₂), et l'autre (x₂,x₁), laissent E stable.

Le groupe des deux permutations est isomorphe au groupe de Galois. Initialement c'est ainsi qu'il était défini. Il est ici isomorphe à Z/2Z. D'autres exemples sont donnés dans l'article Théorème d'Abel-Ruffini.