Hamiltonien de Heisenberg - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Cas des verres de spin - Cas des isolants - Généralisations

Introduction

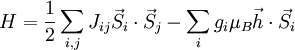
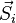
Dans la théorie du magnétisme quantique, l'Hamiltonien de Heisenberg décrit un ensemble de moments magnétiques localisés en interaction. Cet Hamiltonien s'écrit: $H=\frac 1 2 \sum_{i,j} J_{ij} \vec{S}_i \cdot \vec{S}_j - \sum_i g_i \mu_B \vec{h}\cdot \vec{S}_i$ où $μ B$ est le magnéton de Bohr, $g i$ est le rapport gyromagnétique du $i$ -éme moment localisé, $\vec{S}_i$ est un opérateur de spin, $\vec{h}$ est le champ magnétique externe, et $J i j$ est la constante d'échange. Pour $J i j > 0$ l'interaction est antiferromagnétique et pour $J i j < 0$ elle est ferromagnétique. En général, les sites $i$ sont placés sur les nœuds d'un réseau régulier. Une exception est le cas des verres de spin où les moments magnétiques sont des impuretés magnétiques diluées dans un métal non-magnétique (par exemple du fer dilué dans de l'or ou du manganèse dans du cuivre).

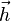
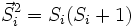
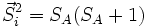
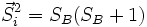
Dans un système sur un réseau bipartite formé de deux sous-réseaux A et B, si les spins $\vec{S}_i^2=S_i(S_i+1)$ n'ont pas tous des $S i$ identiques, par exemple si sur le sous-réseau A $\vec{S}_i^2=S_A(S_A+1)$ et sur le sous-réseau B $\vec{S}_i^2=S_B(S_B+1)$ on parlera d'un modèle ferrimagnétique.

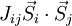
Un concept important dans l'analyse du modèle de Heisenberg est celui de frustration. On dit qu'il y a frustration lorsqu'il n'est pas possible de minimiser indépendamment chaque terme $J_{ij} \vec{S}_i\cdot \vec{S}_j$ . Ce cas peut se présenter soit dans les verres de spin, soit dans des modèles antiferromagnétiques sur le réseau triangulaire ou le réseau Kagomé. Dans ce dernier cas on parle de frustration déterministe.

Cas des verres de spin

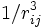
Pour des impuretés diluées dans un métal (le cas des verres de spin), l'interaction $J i j$ est une interaction de Ruddermann-Kittel-Kasuya-Yosida médiée par les électrons de conduction qui décroît avec la distance $r i j$ entre les impuretés comme $1/r_{ij}^3$ et son signe alterne. Il en résulte en particulier que dans un verre de spin, les moments magnétiques n'ont aucune configuration qui minimise toutes les énergies d'échange existantes entre ces moments magnétiques. On parle de frustration. Pour décrire ces interactions aléatoires entre les moments magnétiques, on considère des modèles simplifiés où les ions magnétiques sont placés sur un réseau régulier mais les énergies d'échanges sont aléatoires. Lorsque les interactions aléatoires sont uniquement entre premiers voisins on parle d'un modèle d'Edwards-Anderson. Lorsque les interactions aléatoires sont de portée infinie, on parle d'un modèle de Sherrington-Kirkpatrick.

Cas des isolants

Dans un isolant, l'interaction d'échange décroît exponentiellement avec la distance entre les spins localisés car elle dépend du recouvrement des orbitales. On peut donc se restreindre à des interactions uniquement entre les spins premiers voisins ou entre premier et second voisins. En général, l'interaction est due à un mécanisme de superéchange. Elle est le plus souvent antiferromagnétique. Les règles de Goodenough permettent de prédire le signe des interactions de superéchange dans les oxydes. Si les liaisons entre les ions magnétiques et les ions oxygène font des angles d'environ 180°, l'interaction d'échange entre les ions magnétiques sera antiferromagnétique. Si les angles sont de 90°, les interactions seront ferromagnétiques.

Généralisations

Anisotropies

Dans un cristal, la symétrie est réduite à un groupe d'espace. De ce fait, les interactions entre les spins ne possèdent pas forcément l'invariance par le groupe SU(2). Pour pouvoir décrire correctement les propriétés magnétiques, il devient nécessaire d'utiliser une généralisation du modèle de Heisenberg contenant des termes d'anisotropie.

Single ion

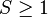
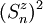
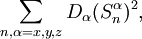
Dans le cas où les spins $S\ge 1$ , les termes $(S_n^z)^2$ ne se réduisent pas à des constantes. Dans un cristal de symétrie suffisamment basse, il peut donc exister dans le Hamiltonien magnétique des termes de la forme: $\sum_{n,\alpha=x,y,z} D_\alpha (S_n^\alpha)^2,$ où on peut supposer que

∑	D_α = 0
α

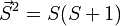
, puisque $\vec{S}^2=S(S+1)$ . Ces termes sont appelés "single-ion anisotropy". Si $D α > 0$ , ils tendent à empêcher l'aimantation de s'aligner sur la direction $α$ .

Échange anisotrope

Il est également possible de rencontrer des interactions de la forme:

Dans le cas le plus général, ce modèle est appelé modèle XYZ. Dans le cas où , et il existe au moins une valeur de $n$ pour laquelle , on parle de modèle XXZ (les directions X et Y étant équivalentes). Lorsque , on parle de modèle XY. Si de plus, , on parle de modèle XX ou XX0. Dans le cas où l'interaction est limitée aux premiers voisins, si $| J z | > | J x | , | J y |$ , le système aura tendance à s'aimanter selon la direction z qui est appelée l'axe facile. Dans le cas XXZ, avec $J x > J z$ , le système s'aimante plutôt dans le plan XY qui est appelé plan facile.

En 1956, Matsubara et Matsuda ont montré que dans le cas d'un spin 1/2, le modèle XXZ est équivalent à un modèle de bosons sur réseau avec répulsion de cœur dur et interaction à deux corps mesurée par . L'apparition d'une aimantation dans le plan dans le modèle XXZ équivaut à la condensation de Bose (ou superfluidité des bosons) tandis que l'apparition d'une aimantation alternée dans le modèle magnétique correspond à un ordre de charge des bosons.

Dzyaloshinskii-Moriya

Lorsqu'il existe une interaction spin-orbite, il est possible de trouver un Hamiltonien magnétique contenant des termes de la forme: , appelés termes de Dzyaloshinskii-Moriya. La présence de ces termes tend à imposer un angle entre les moments magnétiques différent de zéro ou cent-quatre-vingt degrés. En particulier, elle donne lieu dans un milieu antiferromagnétique au ferromagnétisme faible.

Kaplan,Shektman, Entin-Wohlmann et Aharony ont montré que si les interaction entre électrons possèdent la symétrie SU(2), cette symétrie étant préservée dans le Hamiltonien magnétique, il existe aussi nécessairement un terme d'anisotropie supplémentaire dans le Hamiltonien, de la forme , où $D αβ$ est un tenseur de rang 2 symétrique.

Échange cyclique

Dans le cas de $3 H e$ solide, il est possible d'avoir des échanges à trois ou quatre particules. On doit alors généraliser l'Hamiltonien de Heisenberg en ajoutant des termes d'échange cyclique faisant intervenir respectivement trois ou quatre spins.

- Introduction - Cas des verres de spin - Cas des isolants - Généralisations